
【題目】對于定義域為D的函數![]() ,若同時滿足下列條件:①
,若同時滿足下列條件:①![]() 在D內單調遞增或單調遞減;②存在區間
在D內單調遞增或單調遞減;②存在區間![]() ,使
,使![]() 在
在![]() 上的值域為
上的值域為![]() ,則把
,則把![]() 叫閉函數。
叫閉函數。
(1)求閉函數![]() 符合條件②的區間
符合條件②的區間![]() ;
;
(2)判斷函數![]() 是否為閉函數?并說明理由;
是否為閉函數?并說明理由;
(3)已知![]() 是正整數,且定義在
是正整數,且定義在![]() 的函數
的函數![]() 是閉函數,求正整數
是閉函數,求正整數![]() 的最小值,及此時實數k的取值范圍。
的最小值,及此時實數k的取值范圍。
【答案】(1)![]() ;(2)不是,理由見解析;(3)
;(2)不是,理由見解析;(3)![]() 。
。
【解析】
試題分析:(1)由題意,![]() 在
在![]() 上遞減,在
上遞減,在![]() 上的值域為
上的值域為![]() ,故有
,故有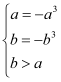 ,求得
,求得![]() 、
、![]() 的值,可得結論;(2)取
的值,可得結論;(2)取![]() ,則由
,則由![]() ,可得
,可得![]() 不是
不是![]() 上的減函數。同理求得
上的減函數。同理求得![]() 不是
不是![]() 上的增函數,從而該函數不是閉函數;(3)由題意,可得方程
上的增函數,從而該函數不是閉函數;(3)由題意,可得方程![]() 在
在![]() 上有兩個不等的實根.利用基本不等式求得當
上有兩個不等的實根.利用基本不等式求得當![]() 時,
時,![]() 取得最小值為
取得最小值為![]() .再根據函數
.再根據函數![]() 在
在![]() 上遞減,在
上遞減,在![]() 遞增,而函數
遞增,而函數![]() 與
與![]() 在
在![]() 有兩個交點,可得正整數
有兩個交點,可得正整數![]() 的最小值為
的最小值為![]() ,此時,
,此時,![]() ,由此求得
,由此求得![]() 的范圍。
的范圍。
試題解析:(1)由題意,![]() 在
在![]() 上遞減,則
上遞減,則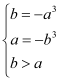 解得
解得![]() 所以,所求的區間為
所以,所求的區間為![]() 。
。
(2)取![]() 則
則![]() ,即
,即![]() 不是
不是![]() 上的減函數。取
上的減函數。取![]()
![]() ,即
,即![]() 不是
不是![]() 上的增函數。所以,函數在定義域內不單調遞增或單調遞減,從而該函數不是閉函數。
上的增函數。所以,函數在定義域內不單調遞增或單調遞減,從而該函數不是閉函數。
(3)![]() 是閉函數,則存在區間
是閉函數,則存在區間![]() ,使函數
,使函數![]() 的值域為
的值域為![]() ,
,![]() 在
在![]() 單調遞增,即
單調遞增,即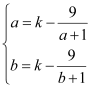 ,
,![]() 為方程
為方程![]() 的兩個實根,即方程
的兩個實根,即方程![]() 在
在![]() 上有兩個不等的實根。
上有兩個不等的實根。![]() ,當且僅當
,當且僅當![]() 時取等號考察函數
時取等號考察函數![]()
∵函數![]() 在
在![]() 上遞減,∴
上遞減,∴![]() 。
。
∵![]() 在
在![]() 遞增,而函數
遞增,而函數![]() 與
與![]() 在
在![]() 有兩個交點。
有兩個交點。
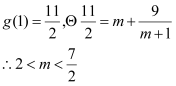
所以正整數![]() 的最小值為
的最小值為![]() ,
,![]() ,此時
,此時![]() 的取值范圍為
的取值范圍為![]() 。
。


 學練快車道快樂假期暑假作業新疆人民出版社系列答案
學練快車道快樂假期暑假作業新疆人民出版社系列答案 浙大優學小學年級銜接導與練浙江大學出版社系列答案
浙大優學小學年級銜接導與練浙江大學出版社系列答案 小學暑假作業東南大學出版社系列答案
小學暑假作業東南大學出版社系列答案 津橋教育暑假拔高銜接廣東人民出版社系列答案
津橋教育暑假拔高銜接廣東人民出版社系列答案科目:高中數學 來源: 題型:
【題目】下列函數中,既是偶函數又在區間(0,+∞)上單調遞增的是( )
A.f(x)=ln|x|
B.f(x)=2﹣x
C.f(x)=x3
D.f(x)=﹣x2
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】比較下列各題中兩個值的大小.
(1)1.82.2 , 1.83;
(2)0.7-0.3 , 0.7-0.4;
(3)1.90.4 , 0.92.4.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列命題中正確的是( )
A. 如果兩條直線都平行于同一個平面,那么這兩條直線互相平行
B. 過一條直線有且只有一個平面與已知平面垂直
C. 如果一條直線平行于一個平面內的一條直線,那么這條直線平行于這個平面
D. 如果兩條直線都垂直于同一平面,那么這兩條直線共面
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2019年10月13日,中國鄭開國際馬拉松賽在鄭東新區開賽.比賽之前,從某大學報名的30名大學生中選8人進行志愿者服務,請分別用抽簽法和隨機數法設計抽樣方案.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一房產商競標得一塊扇形![]() 地皮,其圓心角
地皮,其圓心角![]()
![]() ,半徑為
,半徑為![]()
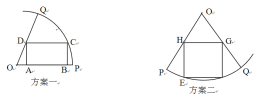
![]() ,房產商欲在此地皮上修建一棟平面圖為矩形的商住樓,為使得地皮的使用率最大,準備了兩種設計方案如圖,方案一:矩形
,房產商欲在此地皮上修建一棟平面圖為矩形的商住樓,為使得地皮的使用率最大,準備了兩種設計方案如圖,方案一:矩形![]() 的一邊
的一邊![]() 在半徑
在半徑![]() 上,
上,![]() 在圓弧上,
在圓弧上,![]() 在半徑
在半徑![]() ;方案二:矩形EFGH的頂點在圓弧上,頂點
;方案二:矩形EFGH的頂點在圓弧上,頂點![]() 分別在兩條半徑上。請你通過計算,為房產商提供決策建議。
分別在兩條半徑上。請你通過計算,為房產商提供決策建議。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知小矩形花壇ABCD中,AB=3m,AD=2m,現要將小矩形花壇建成大矩形花壇AMPN,使點B在AM上,點D在AN上,且對角線MN過點C.

(1)要使矩形AMPN的面積大于32m2,AN的長應在什么范圍內?
(2)M,N是否存在這樣的位置,使矩形AMPN的面積最小?若存在,求出這個最小面積及相應的AM。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某服裝廠生產一種服裝的成本為40元,出廠單價定為60元,該廠為鼓勵銷售商訂購,決定當一次訂購超過100件時,每多訂購1件,訂購的全部服裝的出場單價就降低0.02元,根據市場調查,銷售商一次訂購量不會超過600件.
(1)設銷售一次訂購![]() 件,服裝的實際出廠單價為
件,服裝的實際出廠單價為![]() 元,寫出函數
元,寫出函數![]() 的表達式;
的表達式;
(2)當銷售商一次訂購多少件服裝時,該廠獲得的利潤最大?最大利潤是多少?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com