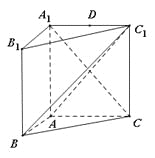
【題目】如圖，在直三棱柱
中，
，且
．
（1）求證：平面
⊥平面
；
（2）設
是
的中點，判斷并證明在線段
上是否存在點
，使
‖平面；若存在，求三棱錐
的體積．
【答案】（1）證明詳見解析；（2）
.
【解析】試題分析：本題以直三棱柱為幾何背景，考查線線垂直、線面垂直、面面垂直、面面平行、線面平行、三棱錐的體積等基礎知識，考查學生的空間想象能力、邏輯推理能力、計算能力.第一問，要證平面
⊥平面
，需要證
平面
；第二問，作出輔助線，通過3邊都平行，利用面面平行的判定得到面EFD//平面，再利用面面平行的性質得DE//平面，由于
平面
，所以
是三棱錐
的高，所以將
轉化為
，再求解.
試題解析：（1）∵直三棱柱側面為矩形，且
，
∴四邊形
為正方形，
∴
，
∵
，
平面，
平面，
∴
平面
∵
平面
∴平面⊥平面； .5分
（2）分別取
，
的中點
，
，連接
，
，
平面
∥平面，
‖平面， .8分
平面
， .10分
.12分
科目：高中數學 來源： 題型：
【題目】下列說法中，正確的個數為（ ）
（1） 
（2）已知向量 
=（6，2）與 
=（﹣3，k）的夾角是鈍角，則k的取值范圍是k＜0
（3）若向量 
能作為平面內所有向量的一組基底
（4）若 
，則 在 上的投影為 
．
A.1個
B.2個
C.3個
D.4個
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】函數y=f（x）的圖象如圖所示．觀察圖象可知函數y=f（x）的定義域、值域分別是（ ）
A.[﹣5，0]∪[2，6），[0，5]
B.[﹣5，6），[0，+∞）
C.[﹣5，0]∪[2，6），[0，+∞）
D.[﹣5，+∞），[2，5]
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設函數f（x）=|x|，g（x）=lg（ax2﹣4x+1），若對任意x1∈R，都存在在x2∈R，使f（x1）=g（x2），則實數a的取值范圍是（ ）
A.（﹣∞，4]
B.（0，4]
C.（﹣4，0]
D.[0，+∞）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】對于函數
、
、
，如果存在實數
使得
，那么稱
為
、
的生成函數．
(1) 下面給出兩組函數， 
是否分別為
、
的生成函數？并說明理由；
第一組： 
， 
， 
第二組： 
， 
， 
；
(2) 設
， 
， 
，生成函數
．若不等式
在
上有解，求實數
的取值范圍；
(3) 設
， 
，取
，生成函數
圖像的最低點坐標為
．若對于任意正實數
，且
，試問是否存在最大的常數
，使
恒成立？如果存在，求出這個
的值；如果不存在，請說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓C： 
=1的離心率為 
，焦距為2，右焦點為F，過點F的直線交橢圓于A、B兩點．
（1）求橢圓C的方程；
（2）在x軸上是否存在定點M，使得 
為定值？若存在，求出定值和定點坐標；若不存在，請說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】函數f（x）=﹣x2+（3﹣2m）x+2+m（0＜m≤1）．
（1）若x∈[0，m]，證明：f（x）≤ 
；
（2）求|f（x）|在[﹣1，1]上的最大值g（m）．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
