【題目】中國古代儒家要求學生掌握六種基本才藝：禮、樂、射、御、書、數，簡稱“六藝”,某高中學校為弘揚“六藝”的傳統文化，分別進行了主題為“禮、樂、射、御、書、數”六場傳統文化知識競賽，現有甲、乙、丙三位選手進入了前三名的最后角逐,規定：每場知識競賽前三名的得分都分別為
且
；選手最后得分為各場得分之和，在六場比賽后，已知甲最后得分為
分，乙和丙最后得分都是
分，且乙在其中一場比賽中獲得第一名，下列說法正確的是( )
A. 乙有四場比賽獲得第三名
B. 每場比賽第一名得分
為
C. 甲可能有一場比賽獲得第二名
D. 丙可能有一場比賽獲得第一名
科目：高中數學 來源： 題型：
【題目】據統計，2017年國慶中秋假日期間，黔東南州共接待游客590.23萬人次，實現旅游收入48.67億元，同比分別增長44.57%、55.22%.旅游公司規定：若公司導游接待旅客，旅游年總收入不低于40（單位：百萬元），則稱為優秀導游.經驗表明，如果公司的優秀導游率越高，則該公司的影響度越高.已知甲、乙兩家旅游公司各有導游100名，統計他們一年內旅游總收入，分別得到甲公司的頻率分布直方圖和乙公司的頻數分布表如下：
分組 |
|
|
|
|
|
頻數 |
| 18 | 49 | 24 | 5 |
（Ⅰ）求
的值，并比較甲、乙兩家旅游公司，哪家的影響度高?
（Ⅱ）若導游的獎金
（單位：萬元），與其一年內旅游總收入
（單位：百萬元）之間的關系為
，求甲公司導游的年平均獎金；
（Ⅲ）從甲、乙兩家公司旅游收入在
的總人數中，用分層抽樣的方法隨機抽取6人進行表彰，其中有兩名導游代表旅游行業去參加座談，求參加座談的導游中有乙公司導游的概率.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某廠生產不同規格的一種產品，根據檢測標準，其合格產品的質量
與尺寸x（mm）之間近似滿足關系式
（b、c為大于0的常數）．按照某項指標測定，當產品質量與尺寸的比在區間
內時為優等品．現隨機抽取6件合格產品，測得數據如下：
尺寸x（mm） | 38 | 48 | 58 | 68 | 78 | 88 |
質量y (g) | 16.8 | 18.8 | 20.7 | 22.4 | 24 | 25.5 |
質量與尺寸的比 | 0.442 | 0.392 | 0.357 | 0.329 | 0.308 | 0.290 |
（Ⅰ）現從抽取的6件合格產品中再任選3件，記
為取到優等品的件數，試求隨機變量的分布列和期望；
（Ⅱ）根據測得數據作了初步處理，得相關統計量的值如下表：
|
|
|
|
75.3 | 24.6 | 18.3 | 101.4 |
（ⅰ）根據所給統計量，求y關于x的回歸方程；
（ⅱ）已知優等品的收益
（單位：千元）與
的關系為
，則當優等品的尺寸x為何值時，收益的預報值最大？（精確到0.1）
附：對于樣本
，其回歸直線
的斜率和截距的最小二乘估計公式分別為：
，
，
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】甲、乙兩支籃球隊賽季總決賽采用7場4勝制，每場必須分出勝負，場與場之間互不影響，只要有一隊獲勝4場就結束比賽．現已比賽了4場，且甲籃球隊勝3場．已知甲球隊第5，6場獲勝的概率均為
，但由于體力原因，第7場獲勝的概率為
．
（1）求甲隊分別以
，
獲勝的概率；
（2）設
表示決出冠軍時比賽的場數，求的分布列及數學期望．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，已知直四棱柱
的底面是直角梯形，
，
，
、
分別是棱
、
上的動點，且
，
，
，
.
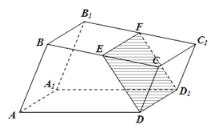
（1）證明：無論點怎樣運動，四邊形
都為矩形；
（2）當
時，求幾何體
的體積.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某同學理科成績優異，今年參加了數學，物理，化學，生物4門學科競賽．已知該同學數學獲一等獎的概率為
，物理，化學，生物獲一等獎的概率都是
，且四門學科是否獲一等獎相互獨立．
（1）求該同學至多有一門學科獲得一等獎的概率；
（2）用隨機變量
表示該同學獲得一等獎的總數，求的概率分布和數學期望
．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
