
���}Ŀ����֪�E�A![]() ��
��![]() �����ҽ��c(di��n)�քe��
�����ҽ��c(di��n)�քe��![]() ��
��![]() ���^ԭ�c(di��n)
���^ԭ�c(di��n)![]() ��б�ʞ�1��ֱ�����E�A
��б�ʞ�1��ֱ�����E�A![]() ��
��![]() ���c(di��n)����߅��
���c(di��n)����߅��![]() �����L�c��e�քe��12�c
�����L�c��e�քe��12�c![]() .
.
��1����E�A![]() �Ę�(bi��o)��(zh��n)���̣�
�Ę�(bi��o)��(zh��n)���̣�
��2��ֱ��![]() �c�A
�c�A![]() �������c�E�A
�������c�E�A![]() ����
����![]() ���c(di��n)����ԭ�c(di��n)��
���c(di��n)����ԭ�c(di��n)��![]() ���д����������x.
������������x.
���𰸡���1��![]() ��2��
��2��![]()
��������
��1�������O(sh��)�c(di��n)![]() �ǵ�һ�����c(di��n)������߅��
�ǵ�һ�����c(di��n)������߅��![]() �����L���
�����L���![]() ����e���
����e���![]() �c
�c![]() �P(gu��n)ϵ�������c(di��n)
�P(gu��n)ϵ�������c(di��n)![]() ��ֱ��
��ֱ��![]() �ϣ��õ�
�ϣ��õ�![]() �c
�c![]() �P(gu��n)ϵ������E�A���̣���⼴�ɣ�
�P(gu��n)ϵ������E�A���̣���⼴�ɣ�
��2�������ֱ��![]() б�ʲ����ڕr(sh��)��ԭ�c(di��n)��
б�ʲ����ڕr(sh��)��ԭ�c(di��n)��![]() ���д����ľ��x��б�ʞ�0�r(sh��)
���д����ľ��x��б�ʞ�0�r(sh��)![]() �c�E�Aֻ��һ��(g��)���c(di��n)��ֱ��
�c�E�Aֻ��һ��(g��)���c(di��n)��ֱ��![]() б�ʴ��ڕr(sh��)���O(sh��)�䷽�̞�
б�ʴ��ڕr(sh��)���O(sh��)�䷽�̞�![]() �������c�A
�������c�A![]() �������
���У����![]() �P(gu��n)ϵ��ֱ��
�P(gu��n)ϵ��ֱ��![]() �����c�E�A����(li��n)�������
�����c�E�A����(li��n)�������![]() ���c(di��n)����(bi��o)���õ�
���c(di��n)����(bi��o)���õ�![]() ���д������̣��M(j��n)�����ԭ�c(di��n)��
���д������̣��M(j��n)�����ԭ�c(di��n)��![]() �д����ľ��x���_(d��)ʽ���Y(ji��)��
�д����ľ��x���_(d��)ʽ���Y(ji��)��![]() �P(gu��n)ϵ����������Y(ji��)Փ.
�P(gu��n)ϵ����������Y(ji��)Փ.
��1�������O(sh��)�c(di��n)![]() �ǵ�һ�����c(di��n)��
�ǵ�һ�����c(di��n)��
��?y��n)���߅�?/span>![]() �����L��12������
�����L��12������![]() ��
��![]() ��
��
��?y��n)?/span>![]() ������
������![]() ��
��
��![]() ���c(di��n)
���c(di��n)![]() ���^ԭ�c(di��n)
���^ԭ�c(di��n)![]() ��б�ʞ�1��ֱ���c�E�A�Ľ��c(di��n)��
��б�ʞ�1��ֱ���c�E�A�Ľ��c(di��n)��
���c(di��n)![]() ��ֱ��
��ֱ��![]() �ϣ��c(di��n)
�ϣ��c(di��n)![]() �ڙE�A
�ڙE�A![]() �ϣ�
�ϣ�
����![]() ����
����![]() ��
��
���![]() ��
��![]() ���ᣩ��
���ᣩ��
���ԙE�A�Ę�(bi��o)��(zh��n)���̞�![]() .
.
��2����(d��ng)ֱ����б�ʲ����ڕr(sh��)��ֱ����![]() ��
��
����![]() �������
���д�����![]() �S��ԭ�c(di��n)��
�S��ԭ�c(di��n)��![]() �S�ľ��x��0.
�S�ľ��x��0.
��(d��ng)ֱ��![]() ��б�ʴ��ڕr(sh��)���O(sh��)б�ʞ�
��б�ʴ��ڕr(sh��)���O(sh��)б�ʞ�![]() �����}����O(sh��)
�����}����O(sh��)![]() ��
��
��?y��n)�ֱ��![]() �c�A
�c�A![]() ��������
��������![]() ��
��
�O(sh��)![]() ��
��![]() ��(li��n)��
��(li��n)��![]() ��
��
��![]() ��
��
��![]() ����
����![]() ������?y��n)?/span>
������?y��n)?/span>![]() ������
������![]() ��
��
����![]() ��
��
����![]() �����c(di��n)����(bi��o)��
�����c(di��n)����(bi��o)��![]() ��
��
����![]() ���д������̞�
���д������̞�![]() ��
��
��������![]() ��
��
ԭ�c(di��n)��ֱ���д����ľ��x ��
��
��(d��ng)�҃H��(d��ng)![]() ����
����![]() �r(sh��)����̖������
�r(sh��)����̖������
����ԭ�c(di��n)��![]() ���д����������x��
������������x��![]() .
.



| �꼉 | �����n�� | �꼉 | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����D��ʾ���������_![]() �У�
��![]() ����
����![]() ����߅��
����߅��![]() �����Σ�
������![]() ��
��![]() .
.
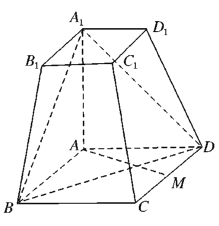
��1����![]() ��
��![]() ���c(di��n)�����C��
���c(di��n)�����C��![]() ƽ��
ƽ��![]() ��
��
��2����ֱ��![]() �cƽ��
�cƽ��![]() ���ɽǵ�����ֵ.
���ɽǵ�����ֵ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ�����и����¼���,�������(d��)���¼�����( )
A.�\(y��n)��(d��ng)�T�����һ��,������9�h(hu��n)���c������8�h(hu��n)��
B.���҃��\(y��n)��(d��ng)�T�����һ��,��������10�h(hu��n)���c��������9�h(hu��n)��
C.���҃��\(y��n)��(d��ng)�T�����һ��,�����Ҷ�����Ŀ��(bi��o)���c�����Ҷ��]������Ŀ��(bi��o)��
D.���҃��\(y��n)��(d��ng)�T�����һ��,��������1������Ŀ��(bi��o)���c��������Ŀ��(bi��o)����δ����Ŀ��(bi��o)��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ���O(sh��)�E�A![]() (
(![]() )���x���ʞ�
)���x���ʞ�![]() ���A
���A![]() �c
�c![]() �S�����S�����c(di��n)
�S�����S�����c(di��n)![]() ���A
���A![]() ���c(di��n)
���c(di��n)![]() ̎���о����E�A
̎���о����E�A![]() �صõ����L��
�صõ����L��![]() ��
��
(��)��E�A![]() �ķ��̣�
�ķ��̣�
(��)�O(sh��)�A![]() ������һ�c(di��n)
������һ�c(di��n)![]() ̎���о����E�A
̎���о����E�A![]() ���c(di��n)
���c(di��n)![]() ��ԇ�Д�
��ԇ�Д�![]() �Ƿ�鶨ֵ�����鶨ֵ�����ԓ��ֵ�������Ƕ�ֵ��Ո�f������.
�Ƿ�鶨ֵ�����鶨ֵ�����ԓ��ֵ�������Ƕ�ֵ��Ո�f������.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����D��ʾ,A,B�քe�ǙE�AC:![]() =1(a>b>0)��������c(di��n),F�����ҽ��c(di��n),2��|AF|�c|FB|�ĵȲ����(xi��ng),
=1(a>b>0)��������c(di��n),F�����ҽ��c(di��n),2��|AF|�c|FB|�ĵȲ����(xi��ng),![]() ��|AF|�c|FB|�ĵȱ����(xi��ng).�c(di��n)P�ǙE�AC�Ϯ���A,B����һ��(d��ng)�c(di��n),�^�c(di��n)A��ֱ��l��x�S.�Ծ���AF��ֱ���ĈA��ֱ��AP���c(di��n)A,M,�B��FM��ֱ��l���c(di��n)Q.
��|AF|�c|FB|�ĵȱ����(xi��ng).�c(di��n)P�ǙE�AC�Ϯ���A,B����һ��(d��ng)�c(di��n),�^�c(di��n)A��ֱ��l��x�S.�Ծ���AF��ֱ���ĈA��ֱ��AP���c(di��n)A,M,�B��FM��ֱ��l���c(di��n)Q.
(1)��E�AC�ķ���;
(2)ԇ����x�S���Ƿ����һ��(g��)���c(di��n)N,ʹ��ֱ��PQ���^ԓ���c(di��n)N?������,����c(di��n)N������(bi��o),��������,�f������.

�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪�E�A![]() ��
��![]() ��
��![]() ��E�A�����ҽ��c(di��n)��
��E�A�����ҽ��c(di��n)��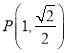 ��E�A��һ�c(di��n)����
��E�A��һ�c(di��n)����![]() .
.
��1����E�A�Ę�(bi��o)��(zh��n)���̣�
��2���O(sh��)ֱ��![]() ���^�c(di��n)
���^�c(di��n)![]() ��ֱ�����E�A��
��ֱ�����E�A��![]() ��
��![]() ���c(di��n)������
���c(di��n)������![]() �Ĵ�ֱƽ�־��քe��ֱ��
�Ĵ�ֱƽ�־��քe��ֱ��![]() ��ֱ��
��ֱ��![]() ��
��![]() ��
��![]() ���c(di��n)����(d��ng)
���c(di��n)����(d��ng)![]() ��С�r(sh��)����ֱ��
��С�r(sh��)����ֱ��![]() �ķ���.
�ķ���.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ���S���ƌW(xu��)���g(sh��)���w�ٰl(f��)չ���W(w��ng)�j(lu��)Ҳ�ѽ�(j��ng)��u�������˂����ճ�����W(w��ng)ُ����һ�N�µ����M(f��i)��ʽ��������п�ݡ���Ʒ�N��Rȫ���ԃr(ji��)�ȸߵȃ�(y��u)�ݶ����V�����M(f��i)���J(r��n)��.ij�W(w��ng)ُ��˾�y(t��ng)Ӌ(j��)�˽������ڱ���˾�W(w��ng)ُ���˔�(sh��)���õ����µ����P(gu��n)��(sh��)��(j��)(������x=1����ʾ2015�꣬��x=2����ʾ2016�꣬������ƣ�y��ʾ�˔�(sh��))��
x | 1 | 2 | 3 | 4 | 5 |
y(�f��) | 20 | 50 | 100 | 150 | 180 |
��1��ԇ����(j��)���еĔ�(sh��)��(j��)�����y�P(gu��n)��x�ľ��Իؚw���̣����A(y��)�y����һ��ԓ��˾�ľW(w��ng)ُ�˔�(sh��)�ܳ��^300�f�ˣ�
��2��ԓ��˾���������W(w��ng)ُ�ߣ��e�Ƴ�����W(w��ng)�j(lu��)�Α������M(f��i)ُ��ȯ�����(d��ng)���W(w��ng)ُ�߿ɸ���(j��)���S���ӵĽY(ji��)�����ٿ����b��܇�ڷ���D�����M(j��n). ���b��܇��Kͣ���������I�����t�W(w��ng)ُ�߿ɫ@�����M(f��i)ُ��ȯ500Ԫ�����b��܇��Kͣ����ʧ���I�����t�W(w��ng)ُ�߿ɫ@�����M(f��i)ُ��ȯ200Ԫ. ��֪���ӳ��F(xi��n)�攵(sh��)�cż��(sh��)�ĸ��ʶ���![]() ������D�Ϙ�(bi��o)�е�0��1��2��������20���b��܇�_ʼ�ڵ�0�W(w��ng)ُ��ÿ���Sһ�����ӣ��b��܇��ǰ�Ƅ�(d��ng)һ��.���S���攵(sh��)���b��܇��ǰ�Ƅ�(d��ng)һ��
������D�Ϙ�(bi��o)�е�0��1��2��������20���b��܇�_ʼ�ڵ�0�W(w��ng)ُ��ÿ���Sһ�����ӣ��b��܇��ǰ�Ƅ�(d��ng)һ��.���S���攵(sh��)���b��܇��ǰ�Ƅ�(d��ng)һ��![]() ��
��![]() �����S��ż��(sh��)�b��܇��ǰ�Ƅ�(d��ng)�ɸ�
�����S��ż��(sh��)�b��܇��ǰ�Ƅ�(d��ng)�ɸ�![]() ��
��![]() ����ֱ���b��܇�Ƶ���19������I�����20��ʧ���I���r(sh��)���Α�Y(ji��)�����O(sh��)�b��܇�Ƶ���
����ֱ���b��܇�Ƶ���19������I�����20��ʧ���I���r(sh��)���Α�Y(ji��)�����O(sh��)�b��܇�Ƶ���![]() ��ĸ��ʞ�
��ĸ��ʞ�![]() ��ԇ�C��
��ԇ�C��![]() �ǵȱȔ�(sh��)�У�����W(w��ng)ُ�߅��c�Α�һ�Ϋ@�����M(f��i)ُ��ȯ���~������ֵ.
�ǵȱȔ�(sh��)�У�����W(w��ng)ُ�߅��c�Α�һ�Ϋ@�����M(f��i)ُ��ȯ���~������ֵ.
�����ھ��Իؚw����![]() �У�
�У�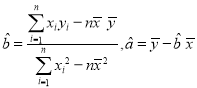 .
.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����������D����ֱ������![]() �У�
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ���c(di��n)
���c(di��n)![]() ��
��![]() �ϣ���
�ϣ���![]() ����
����![]() ��
��![]() ���𣬵õ������F
���𣬵õ������F![]() ���������҈D��.
���������҈D��.
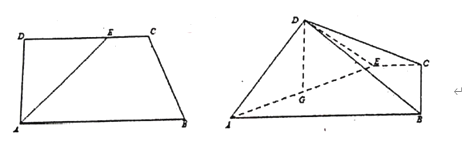
��1���������F![]() ���w�e�����ֵ��
���w�e�����ֵ��
��2���ھ���![]() ���Ƿ�����c(di��n)
���Ƿ�����c(di��n)![]() ��ʹ��
��ʹ��![]() ƽ��
ƽ��![]() �������ڣ���
�������ڣ���![]() ��ֵ���������ڣ�Ո�f������.
��ֵ���������ڣ�Ո�f������.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
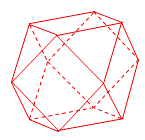
���}Ŀ�����������w(semiregular solid)��Q�������¶����w������D��ʾ������߅��(sh��)��ȫ��ͬ������߅�Ξ���Ķ����w���w�F(xi��n)�˔�(sh��)�W(xu��)�Č��Q�����������w�ؽ���һ��c(di��n)�����l������c(di��n)��ȥһ��(g��)�����F����˹��ɽ�ȥ�˂�(g��)�����F���õ�һ��(g��)��ʮ�Ă�(g��)��İ��������w��������߅�L����ȣ����а˂�(g��)���������Σ�����(g��)�������Σ��Q�@�ӵİ��������w���ʮ�ĵ�߅�w.����ʮ�ĵ�߅�w�����L��![]() ���tԓ��ʮ�ĵ�߅�w�����ı���e�飨 ��
���tԓ��ʮ�ĵ�߅�w�����ı���e�飨 ��
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
���H�W(xu��)У��(y��u)�x - ����(x��)���б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_ | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com