Question

【題目】已知函數f（x）=lnx﹣mx（m∈R）．
（1）討論函數f（x）的單調區間；
（2）當m≥ 時，設g（x）=2f（x）+x2的兩個極值點x1 ， x2（x1＜x2）恰為h（x）=lnx﹣cx2﹣bx的零點，求y=（x1﹣x2）h′（ ）的最小值．

Answer 1

【答案】
（1）解：∵函數f（x）=lnx﹣mx，∴ ，x＞0；

當m＞0時，由1﹣mx＞0解得x＜ ，即當0＜x＜ 時，f'（x）＞0，f（x）單調遞增；

由1﹣mx＜0解得x＞ ，即當x＞ 時，f'（x）＜0，f（x）單調遞減；

當m=0時，f'（x）= ＞0，即f（x）在（0，+∞）上單調遞增；

當m＜0時，1﹣mx＞0，故f'（x）＞0，即f（x）在（0，+∞）上單調遞增；

∴當m＞0時，f（x）的單調遞增區間為（0， ），單調遞減區間為（ ，+∞）；

當m≤0時，f（x） 的單調遞增區間為（0，+∞）； …（5分）

（2）解：g（x）=2f（x）+x2=2lnx﹣2mx+x2，則 ，

∴g'（x）的兩根x1，x2即為方程x2﹣mx+1=0的兩根；

又∵m≥ ，

∴△=m2﹣4＞0，x1+x2=m，x1x2=1；

又∵x1，x2為h（x）=lnx﹣cx2﹣bx的零點，

∴lnx1﹣cx12﹣bx1=0，lnx2﹣cx22﹣bx2=0，

兩式相減得 ﹣c（x1﹣x2）（x1+x2）﹣b（x1﹣x2）=0，

得b= ，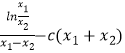

而 ，

∴y=

= ]

= = ，

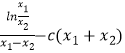令 （0＜t＜1），

由（x1+x2）2=m2得x12+x22+2x1x2=m2，

因為x1x2=1，兩邊同時除以x1x2，得t+ +2=m2，

∵m≥ ，故t+ ≥ ，解得t≤ 或t≥2，∴0＜t≤ ；

設G（t）= ，

∴G'（t）= ，則y=G（t）在（0， ]上是減函數，

∴G（t）min=G（ ）=﹣ +ln2，

即 的最小值為﹣ +ln2

【解析】（1）求出函數f（x）的導數，討論m的取值，利用導數判斷函數f（x）的單調性與單調區間；（2）對函數g（x）求導數，利用極值的定義得出g'（x）=0時存在兩正根x1 ， x2；
再利用判別式以及根與系數的關系，結合零點的定義，構造函數，利用導數即可求出函數y的最小值．
【考點精析】本題主要考查了利用導數研究函數的單調性和函數的極值與導數的相關知識點，需要掌握一般的,函數的單調性與其導數的正負有如下關系： 在某個區間內，(1)如果，那么函數在這個區間單調遞增；(2)如果，那么函數在這個區間單調遞減；求函數的極值的方法是:（1）如果在附近的左側,右側,那么是極大值（2）如果在附近的左側,右側,那么是極小值才能正確解答此題．