
【題目】如圖,已知![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 的中點
的中點
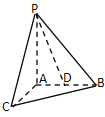
(1)求![]() 與
與![]() 所成角的大小
所成角的大小
(2)求![]() 與平面
與平面![]() 所成的角的大小
所成的角的大小
(3)求![]() 繞直線
繞直線![]() 旋轉一周所構成的旋轉體的體積
旋轉一周所構成的旋轉體的體積
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)取![]() 中點
中點![]() ,由平行關系知所求角為
,由平行關系知所求角為![]() ;在
;在![]() 中求得
中求得![]() ,利用勾股定理可求得
,利用勾股定理可求得![]() 三邊長,由余弦定理得到
三邊長,由余弦定理得到![]() ,進而得到結果;
,進而得到結果;
(2)由線面垂直的判定方法可證得![]() 平面
平面![]() ,由線面角定義知所求角為
,由線面角定義知所求角為![]() ,在
,在![]() 中由長度關系得到
中由長度關系得到![]() ,進而求得結果;
,進而求得結果;
(3)由旋轉特點可知得到的旋轉體為一個大圓錐挖去一個小圓錐,結合圓錐體積公式可求得結果.
(1)取![]() 中點
中點![]() ,連接
,連接![]()
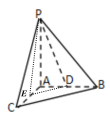
![]() 分別為
分別為![]() 中點
中點 ![]()
![]() 異面直線
異面直線![]() 與
與![]() 所成角即為
所成角即為![]() 與
與![]() 所成角,即
所成角,即![]()
又![]() ,
,![]()
![]() ,
,![]()
![]() ,
,![]() ,
,![]()
![]()
![]()
即異面直線![]() 與
與![]() 所成角為
所成角為![]()
(2)![]() 平面
平面![]() ,
,![]() 平面
平面![]()
![]()
又![]() ,
,![]() 平面
平面![]() ,
,![]()
![]() 平面
平面![]()
![]() 即為
即為![]() 與平面
與平面![]() 所成角
所成角
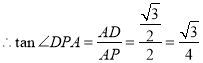
![]()
即![]() 與平面
與平面![]() 所成角為
所成角為![]()
(3)由題意知,所得旋轉體是以![]() 為底面半徑,
為底面半徑,![]() 為高的圓錐中挖去一個以
為高的圓錐中挖去一個以![]() 為底面半徑,
為底面半徑,![]() 為高的小圓錐
為高的小圓錐
![]() 所得旋轉體體積
所得旋轉體體積![]()


科目:高中數學 來源: 題型:
【題目】已知等差數列![]() 的前
的前![]() 項和為
項和為![]() ,集合
,集合![]() ,集合B={
,集合B={![]()
![]() x2﹣y2=1,x,y∈R},請判斷下列三個命題的真假.若為真,請給予證明;若為假,請舉出反例.
x2﹣y2=1,x,y∈R},請判斷下列三個命題的真假.若為真,請給予證明;若為假,請舉出反例.
(1)以集合![]() 中的元素為坐標的點均在同一條直線上;
中的元素為坐標的點均在同一條直線上;
(2)A∩B至多有一個元素;
(3)當a1≠0時,一定有A∩B≠..
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,長度為2的線段EF的兩端點E、F分別在兩坐標軸上運動.
中,長度為2的線段EF的兩端點E、F分別在兩坐標軸上運動.
(1)求線段EF的中點G的軌跡C的方程;
(2)設軌跡C與![]() 軸交于
軸交于![]() 兩點,P是軌跡C上異于
兩點,P是軌跡C上異于![]() 的任意一點,直線
的任意一點,直線![]() 交直線
交直線![]() 于M點,直線
于M點,直線![]() 交直線
交直線![]() 于N點,求證:以MN為直徑的圓C總過定點,并求出定點坐標.
于N點,求證:以MN為直徑的圓C總過定點,并求出定點坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的左、右焦點為別為F1、F2,且過點
的左、右焦點為別為F1、F2,且過點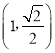 和
和 .
.

(1)求橢圓的標準方程;
(2)如圖,點A為橢圓上一位于x軸上方的動點,AF2的延長線與橢圓交于點B,AO的延長線與橢圓交于點C,求△ABC面積的最大值,并寫出取到最大值時直線BC的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】唐三彩,中國古代陶瓷燒制工藝的珍品,它吸取了中國國畫、雕塑等工藝美術的特點,在中國文化中占有重要的歷史地位,在中國的陶瓷史上留下了濃墨重彩的一筆.唐三彩的生產至今已有![]() 多年的歷史,對唐三彩的復制和仿制工藝,至今也有百余年的歷史.某陶瓷廠在生產過程中,對仿制的
多年的歷史,對唐三彩的復制和仿制工藝,至今也有百余年的歷史.某陶瓷廠在生產過程中,對仿制的![]() 件工藝品測得重量(單位:
件工藝品測得重量(單位:![]() )數據如下表:
)數據如下表:
分組 | 頻數 | 頻率 |
|
|
|
|
| |
|
| |
|
|
|
|
| |
|
| |
合計 |
|
(1)求出頻率分布表中實數![]() ,
,![]() 的值;
的值;
(2)若從仿制的![]() 件工藝品重量范圍在
件工藝品重量范圍在![]() 的工藝品中隨機抽選
的工藝品中隨機抽選![]() 件,求被抽選
件,求被抽選![]() 件工藝品重量均在范圍
件工藝品重量均在范圍![]() 中的概率.
中的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() :曲線
:曲線![]() 表示雙曲線;
表示雙曲線;![]() :曲線
:曲線![]() 表示焦點在
表示焦點在![]() 軸上的橢圓.
軸上的橢圓.
(1)分別求出條件![]() 中的實數
中的實數![]() 的取值范圍;
的取值范圍;
(2)甲同學認為“![]() 是
是![]() 的充分條件”,乙同學認為“
的充分條件”,乙同學認為“![]() 是
是![]() 的必要條件”,請判斷兩位同學的說法是否正確,并說明理由.
的必要條件”,請判斷兩位同學的說法是否正確,并說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com