【題目】蘇州市一木地板廠生產A、B、C三類木地板，每類木地板均有環保型和普通兩種型號，某月的產量如下表（單位：片）：
類型 | 木地板A | 木地板B | 木地板C |
環保型 | 150 | 200 | Z |
普通型 | 250 | 400 | 600 |
按分層抽樣的方法在這個月生產的木地板中抽取50片，其中A類木地板10片．
（1）求Z的值；
（2）用隨機抽樣的方法從B類環保木地板抽取8片，作為一個樣本，經檢測它們的得分如下：9.4、8.6、9.2、9.6、8.7、9.3、9.0、8.2，從中任取一個數，求該數與樣本平均數之差的絕對不超過0.5的概率．
挑戰100單元檢測試卷系列答案科目：高中數學 來源： 題型：
【題目】已知函數f（x）= 
．
（1）求f（x）+f（1﹣x）的值；
（2）若數列{an}滿足an=f（0）+f（ 
）+f（ 
）+…+f（ 
）+f（1）（n∈N*），求數列{an}的通項公式；
（3）若數列{bn}滿足bn=2nan ， Sn是數列{bn}的前n項和，是否存在正實數k，使不等式knSn＞3bn對于一切的n∈N*恒成立？若存在，請求出k的取值范圍；若不存在，請說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知數列{an}中各項都大于1，前n項和為Sn ， 且滿足an2+3an=6Sn﹣2．
（1）求數列{an}的通項公式；
（2）令bn= 
，求數列{bn}的前n項和Tn；
（3）求使得Tn＜ 
對所有n∈N*都成立的最小正整數m．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】袋子A和B中裝有若干個均勻的紅球和白球，從A中摸出一個紅球的概率是 
，從B中摸出一個紅球的概率為p．
（1）從A中又放回的摸球，每次摸出一個，共摸5次 ①恰好有3次摸到紅球的概率；
②第一次、第三次、第五次摸到紅球的概率．
（2）若A、B兩個袋子中的球之比為12，將A、B中的球裝在一起后，從中摸出一個紅球的概率是 
，求p的值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】以直角坐標系的原點為極點O，
軸正半軸為極軸，已知點P的直角坐標為(1,-5),點C的極坐標為
,若直線l經過點P,且傾斜角為
，圓C的半徑為4.
(1).求直線l的參數方程及圓C的極坐標方程;
(2).試判斷直線l與圓C有位置關系.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某省的一個氣象站觀測點在連續4天里記錄的
指數
與當天的空氣水平可見度
（單位： 
）的情況如表1：
該省某市2016年11月
指數頻數分布如表2：
|
|
|
|
|
|
頻數 | 3 | 6 | 12 | 6 | 3 |
（1）設
，根據表1的數據，求出
關于
的線性回歸方程；
（附參考公式： 
，其中
， 
）
（2）小李在該市開了一家洗車店，經統計，洗車店平均每天的收入與
指數由相關關系，如表3：
|
|
|
|
|
|
日均收入（元） |
|
|
|
|
|
根據表3估計小李的洗車店該月份平均每天的收入．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在對某漁業產品的質量調研中，從甲、乙兩地出產的該產品中各隨機抽取10件，測量該產品中某種元素的含量（單位：毫克）．如圖是測量數據的莖葉圖：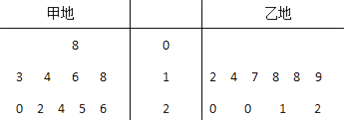 
規定：當產品中的此種元素含量≥15毫克時為優質品．
（Ⅰ）試用上述樣本數據估計甲、乙兩地該產品的優質品率（優質品件數/總件數）；
（Ⅱ）從乙地抽出的上述10件產品中，隨機抽取3件，求抽到的3件產品中優質品數ξ的分布列及數學期望E（ξ）．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
