
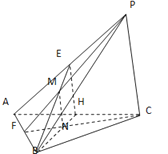
【題目】如圖,在三棱錐![]() 中,
中,![]() 是邊長為2的正三角形,
是邊長為2的正三角形,![]() ,E、F、H分別為AP、AB、AC的中點,PF交BE于點M,CF交BH于點N,
,E、F、H分別為AP、AB、AC的中點,PF交BE于點M,CF交BH于點N,![]() ,
,![]() .
.
![]() 求證:
求證:![]() 平面BEH;
平面BEH;
![]() 求證:
求證:![]() ;
;
![]() 求直線PA與平面ABC所成角的正弦值.
求直線PA與平面ABC所成角的正弦值.
【答案】(1)證明見解析;(2)證明見解析;(3)![]() 。
。
【解析】
(1)推導出BH⊥AC,EH⊥AC,由此能證明AC⊥平面BEH.
(2)推導出N是△ABC的重心,M是△ABP的重心,從而![]() ,由此能證明PC∥MN.
,由此能證明PC∥MN.
(3)取BH的中點G,連結AG,推導出EG⊥BH,EG⊥AC,EG⊥平面ABC,從而∠EAG是PA與平面ABC所成角,由此能求出直線PA與平面ABC所成角的正弦值.
證明:![]() 是邊長為2的正三角形,H是AC中點,
是邊長為2的正三角形,H是AC中點,
![]() ,
,
![]() ,E、H分別為AP、AC的中點,
,E、H分別為AP、AC的中點,
![]() ,
,![]() ,
,
![]() ,
,![]() 平面BEH.
平面BEH.
證明:![]() 交BE于點M,CF交BH于點N,
交BE于點M,CF交BH于點N,
![]() 是邊長為2的正三角形,
是邊長為2的正三角形,![]() ,E、F、H分別為AP、AB、AC的中點,
,E、F、H分別為AP、AB、AC的中點,
![]() 是
是![]() 的重心,
的重心,![]() ,M是
,M是![]() 的重心,
的重心,![]() ,
,
![]() ,
,![]() .
.
![]() 取BH的中點G,連結AG,
取BH的中點G,連結AG,
![]() ,
,![]() ,
,
![]() 平面BEH,
平面BEH,![]() ,
,![]() 平面ABC,
平面ABC,
![]() 是PA與平面ABC所成角,
是PA與平面ABC所成角,
在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
![]() 直線PA與平面ABC所成角的正弦值為
直線PA與平面ABC所成角的正弦值為![]() .
.


 53隨堂測系列答案
53隨堂測系列答案科目:高中數學 來源: 題型:
【題目】如圖,在正方體ABCD﹣A1B1C1D1中,棱長為2,M,N分別為A1B,AC的中點.
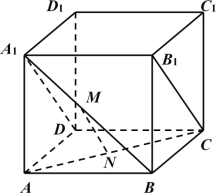
(1)證明:MN//B1C;
(2)求A1B與平面A1B1CD所成角的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,橢圓![]() :
:![]() 與圓
與圓![]() :
:![]() 相切,并且橢圓
相切,并且橢圓![]() 上動點與圓
上動點與圓![]() 上動點間距離最大值為
上動點間距離最大值為![]() .
.

(1)求橢圓![]() 的方程;
的方程;
(2)過點![]() 作兩條互相垂直的直線
作兩條互相垂直的直線![]() ,
,![]() ,
,![]() 與
與![]() 交于
交于![]() 兩點,
兩點,![]() 與圓
與圓![]() 的另一交點為
的另一交點為![]() ,求
,求![]() 面積的最大值,并求取得最大值時直線
面積的最大值,并求取得最大值時直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】市面上有某品牌![]() 型和
型和![]() 型兩種節能燈,假定
型兩種節能燈,假定![]() 型節能燈使用壽命都超過5000小時,經銷商對
型節能燈使用壽命都超過5000小時,經銷商對![]() 型節能燈使用壽命進行了調查統計,得到如下頻率分布直方圖:
型節能燈使用壽命進行了調查統計,得到如下頻率分布直方圖:

某商家因原店面需要重新裝修,需租賃一家新店面進行周轉,合約期一年.新店面需安裝該品牌節能燈5支(同種型號)即可正常營業.經了解,![]() 型20瓦和
型20瓦和![]() 型55瓦的兩種節能燈照明效果相當,都適合安裝.已知
型55瓦的兩種節能燈照明效果相當,都適合安裝.已知![]() 型和
型和![]() 型節能燈每支的價格分別為120元、25元,當地商業電價為0.75元/千瓦時.假定該店面一年周轉期的照明時間為3600小時,若正常營業期間燈壞了立即購買同型燈管更換.(用頻率估計概率)
型節能燈每支的價格分別為120元、25元,當地商業電價為0.75元/千瓦時.假定該店面一年周轉期的照明時間為3600小時,若正常營業期間燈壞了立即購買同型燈管更換.(用頻率估計概率)
(Ⅰ)根據頻率直方圖估算![]() 型節能燈的平均使用壽命;
型節能燈的平均使用壽命;
(Ⅱ)根據統計知識知,若一支燈管一年內需要更換的概率為![]() ,那么
,那么![]() 支燈管估計需要更換
支燈管估計需要更換![]() 支.若該商家新店面全部安裝了
支.若該商家新店面全部安裝了![]() 型節能燈,試估計一年內需更換的支數;
型節能燈,試估計一年內需更換的支數;
(Ⅲ)若只考慮燈的成本和消耗電費,你認為該商家應選擇哪種型號的節能燈,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】有![]() 名學生排成一排,求分別滿足下列條件的排法種數,要求列式并給出計算結果.
名學生排成一排,求分別滿足下列條件的排法種數,要求列式并給出計算結果.
(1)甲不在兩端;
(2)甲、乙相鄰;
(3)甲、乙、丙三人兩兩不得相鄰;
(4)甲不在排頭,乙不在排尾。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓![]() 與直線
與直線![]() 相切,圓心在
相切,圓心在![]() 軸上,且直線
軸上,且直線![]() 被圓
被圓![]() 截得的弦長為
截得的弦長為![]() .
.
(1)求圓![]() 的方程;
的方程;
(2)過點![]() 作斜率為
作斜率為![]() 的直線
的直線![]() 與圓
與圓![]() 交于
交于![]() 兩點,若直線
兩點,若直線![]() 與
與![]() 的斜率乘積為
的斜率乘積為![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com