在一次聯(lián)考后，某校對甲、乙兩個文科班的數(shù)學考試成績進行分析，規(guī)定：大于或等于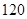
分為優(yōu)秀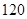，分以下為非優(yōu)秀，統(tǒng)計成績后，得到如下的
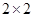列聯(lián)表，且已知在甲、乙兩個文科班全部
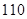人中隨機抽取人為優(yōu)秀的概率為
.
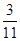| | 優(yōu)秀 | 非優(yōu)秀 | 合計 |
| 甲班 |  | | |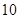
| 乙班 | |  | |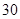
| 合計 | | | |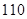
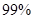的把握認為成績與班級有關系？
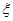表示抽得甲班的學生人數(shù)，求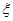的分布列. （1）詳見解析；（2）按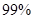的可靠性要求，能認為“成績與班級有關系”；
（3）抽到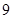
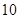或號的概率為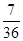
.
解析試題分析：（1）先根據(jù)題中條件確定乙班優(yōu)秀的人數(shù)，然后根據(jù)甲乙兩班的總?cè)藬?shù)將表中其它的數(shù)據(jù)補充上；（2）先提出假設“成績與班級無關”，根據(jù)表中數(shù)據(jù)求出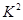
的值，然后利用臨界值表確定犯錯誤的概率，進而確定是否有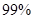的把握認為成績與班級有關系；（3）先確定隨機變量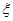的可能取值，然后根據(jù)超幾何分布的方法求出隨機變量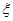在相應的取值下的概率，并列出相應的分布列.
試題解析：（1）列聯(lián)表如下表所示：
（2）假設成績與班級無關，根據(jù)列聯(lián)表中的數(shù)據(jù)，得到 優(yōu)秀 非優(yōu)秀 合計 甲班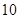 
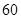
乙班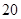 
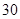
合計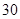 
，
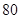
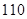
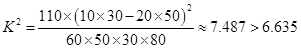因此按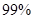的可靠性要求，能認為“成績與班級有關系”；
（3）由（1）知，甲、乙兩個理科班優(yōu)秀的學生人數(shù)分別為、，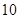
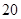依題意得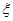，的可能取值為
、
、
，
，
，
，
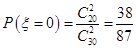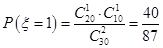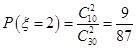所以的分布列為：
名同學,現(xiàn)測得排球隊
)分別是:
、
、
、
、
、
、
、
、
、
、
、
、
、
、
、
,求
的函數(shù)：
，
，
，
，
，
.
的分布列和數(shù)學期望．
表示，椐統(tǒng)計，隨機變量
表示經(jīng)銷一輛汽車的利潤.
的值；
:“購買該品牌汽車的3位顧客中,至多有1位采用3期付款”的概率
；(3)求
.
,
,
,
,
五個等級.現(xiàn)從一批該產(chǎn)品隨機抽取20個，對其等級進行統(tǒng)計分析，得到頻率分布表如下： 
表示游客在甲、乙、丙三處旅游景點中選擇游玩的景點數(shù)和沒有選擇游玩的景點數(shù)的乘積.
是R上的偶函數(shù)”為事件A，求事件A的概率；
的概率分布列及數(shù)學期望.
