
【題目】已知橢圓![]() 與拋物線
與拋物線![]() 共焦點
共焦點![]() ,拋物線上的點M到y軸的距離等于
,拋物線上的點M到y軸的距離等于![]() ,且橢圓與拋物線的交點Q滿足
,且橢圓與拋物線的交點Q滿足![]() .
.
(I)求拋物線的方程和橢圓的方程;
(II)過拋物線上的點![]() 作拋物線的切線
作拋物線的切線![]() 交橢圓于
交橢圓于![]() 、
、![]() 兩點,設(shè)線段AB的中點為
兩點,設(shè)線段AB的中點為![]() ,求
,求![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】試題分析:(1)將拋物線上的點![]() 到
到![]() 軸的距離等于
軸的距離等于![]() 和拋物線的定義相結(jié)合,可得
和拋物線的定義相結(jié)合,可得![]() ,可得拋物線的方程,已知在橢圓中
,可得拋物線的方程,已知在橢圓中![]() 的值,由
的值,由![]() 可得點Q的坐標,結(jié)合橢圓的定義可得橢圓的方程;(2)聯(lián)立直線與拋物線的方程,結(jié)合其有一個交點可得關(guān)系式
可得點Q的坐標,結(jié)合橢圓的定義可得橢圓的方程;(2)聯(lián)立直線與拋物線的方程,結(jié)合其有一個交點可得關(guān)系式![]() ,聯(lián)立直線與橢圓的方程根據(jù)橢圓與直線有2個交點即
,聯(lián)立直線與橢圓的方程根據(jù)橢圓與直線有2個交點即![]() ,得到關(guān)于
,得到關(guān)于![]() 不等式,解不等式可得
不等式,解不等式可得![]() 的取值范圍,由中點坐標公式及韋達定理可得
的取值范圍,由中點坐標公式及韋達定理可得![]() ,從而可得其范圍.
,從而可得其范圍.
試題解析:(1)∵拋物線上的點![]() 到
到![]() 軸的距離等于
軸的距離等于![]() ,
,
∴點M到直線![]() 的距離等于點
的距離等于點![]() 到焦點
到焦點![]() 的距離,
的距離,
得![]() 是拋物線
是拋物線![]() 的準線,即
的準線,即![]() ,
,
解得![]() ,∴拋物線的方程為
,∴拋物線的方程為![]() ;
;
可知橢圓的右焦點![]() ,左焦點
,左焦點![]() ,
,
由![]() 得
得![]() ,又
,又![]() ,解得
,解得![]() ,
,
由橢圓的定義得![]() ,
,
∴![]() ,又
,又![]() ,得
,得![]() ,
,
∴橢圓的方程為![]() .
.
(2)顯然![]() ,
, ![]() ,
,
由![]() ,消去
,消去![]() ,得
,得![]() ,
,
由題意知![]() ,得
,得![]() ,
,
由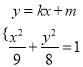 ,消去
,消去![]() ,得
,得![]() ,
,
其中![]() ,
,
化簡得![]() ,
,
又![]() ,得
,得![]() ,解得
,解得![]() ,
,
設(shè)![]() ,則
,則![]() <0,
<0,
由![]() ,得
,得![]() ,∴
,∴![]() 的取值范圍是
的取值范圍是![]() .
.


科目:高中數(shù)學(xué) 來源: 題型:
【題目】函數(shù)f(x)= ![]() +
+ ![]() 的定義域為( )
的定義域為( )
A.[﹣2,0)∪(0,2]
B.(﹣1,0)∪(0,2]
C.[﹣2,2]
D.(﹣1,2]
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某研究小組在電腦上進行人工降雨模擬實驗,準備用A、B、C三種人工降雨方式分別對甲、乙、丙三地實施人工降雨,其實驗統(tǒng)計結(jié)果如下
方式 | 實施地點 | 大雨 | 中雨 | 小雨 | 模擬實驗次數(shù) |
A | 甲 | 2次 | 6次 | 4次 | 12次 |
B | 乙 | 3次 | 6次 | 3次 | 12次 |
C | 丙 | 2次 | 2次 | 8次 | 12次 |
假定對甲、乙、丙三地實施的人工降雨彼此互不影響,且不考慮洪澇災(zāi)害,請根據(jù)統(tǒng)計數(shù)據(jù):
(1)求甲、乙、丙三地都恰為中雨的概率;
(2)考慮不同地區(qū)的干旱程度,當雨量達到理想狀態(tài)時,能緩解旱情,若甲、丙地需中雨或大雨即達到理想狀態(tài),乙地必須是大雨才達到理想狀態(tài),記“甲、乙、丙三地中緩解旱情的個數(shù)”為隨機變量![]() ,求
,求![]() 的分布列和數(shù)學(xué)期望.
的分布列和數(shù)學(xué)期望.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知⊙![]() :
: ![]() 與⊙
與⊙![]() :
: ![]() ,以
,以![]() ,
, ![]() 分別為左右焦點的橢圓
分別為左右焦點的橢圓![]() :
: ![]() 經(jīng)過兩圓的交點.
經(jīng)過兩圓的交點.
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)![]() ,
, ![]() 分別為橢圓
分別為橢圓![]() 的左右頂點,
的左右頂點, ![]() ,
, ![]() ,
, ![]() 是橢圓
是橢圓![]() 上非頂點的三點,若
上非頂點的三點,若![]() ∥
∥![]() ,
, ![]() ∥
∥![]() ,試問
,試問![]() 的面積是否為定值?若是,求出這個定值;若不是,請說明理由.
的面積是否為定值?若是,求出這個定值;若不是,請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】《九章算術(shù)》中有這樣一則問題:“今有良馬與弩馬發(fā)長安,至齊,齊去長安三千里,良馬初日行一百九十三里,日增一十三里;弩馬初日行九十七里,日減半里,良馬先至齊,復(fù)還迎弩馬.”則現(xiàn)有如下說法:
①弩馬第九日走了九十三里路;
②良馬前五日共走了一千零九十五里路;
③良馬和弩馬相遇時,良馬走了二十一日.
則以上說法錯誤的個數(shù)是( )個
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】為了普及環(huán)保知識,增強環(huán)保意識,某校從理科甲班抽取60人,從文科乙班抽取50人參加環(huán)保知識測試.
優(yōu)秀人數(shù) | 非優(yōu)秀人數(shù) | 總計 | |
甲班 | |||
乙班 | 30 | ||
總計 | 60 |
(Ⅰ)根據(jù)題目完成![]() 列聯(lián)表,并據(jù)此判斷是否有
列聯(lián)表,并據(jù)此判斷是否有![]() 的把握認為環(huán)保知識成績優(yōu)秀與學(xué)生的文理分類有關(guān).
的把握認為環(huán)保知識成績優(yōu)秀與學(xué)生的文理分類有關(guān).
(Ⅱ)現(xiàn)已知![]() ,
, ![]() ,
, ![]() 三人獲得優(yōu)秀的概率分別為
三人獲得優(yōu)秀的概率分別為![]() ,
, ![]() ,
, ![]() ,設(shè)隨機變量
,設(shè)隨機變量![]() 表示
表示![]() ,
, ![]() ,
, ![]() 三人中獲得優(yōu)秀的人數(shù),求
三人中獲得優(yōu)秀的人數(shù),求![]() 的分布列及期望
的分布列及期望![]() .
.
附:  ,
, ![]()
| 0.100 | 0.050 | 0.025 | 0.010 | 0.005 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)f(x)=1+ ![]() .
.
(1)求f(x)的定義域;
(2)判斷f(x)的奇偶性,并證明;
(3)求f(x)的值域.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】下列幾個命題
①奇函數(shù)的圖象一定通過原點
②函數(shù)y= ![]() 是偶函數(shù),但不是奇函數(shù)
是偶函數(shù),但不是奇函數(shù)
③函數(shù)f(x)=ax﹣1+3的圖象一定過定點P,則P點的坐標是(1,4)
④若f(x+1)為偶函數(shù),則有f(x+1)=f(﹣x﹣1)
⑤若函數(shù)f(x)= 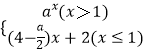 在R上的增函數(shù),則實數(shù)a的取值范圍為[4,8)
在R上的增函數(shù),則實數(shù)a的取值范圍為[4,8)
其中正確的命題序號為 .
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知拋物線![]() :
: ![]() 的焦點為
的焦點為![]() ,圓
,圓![]() :
: ![]() .直線
.直線![]() 與拋物線
與拋物線![]() 交于點
交于點![]() 、
、![]() 兩點,與圓
兩點,與圓![]() 切于點
切于點![]() .
.
(1)當切點![]() 的坐標為
的坐標為![]() 時,求直線
時,求直線![]() 及圓
及圓![]() 的方程;
的方程;
(2)當![]() 時,證明:
時,證明: ![]() 是定值,并求出該定值.
是定值,并求出該定值.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com