
【題目】有以下命題:
①若f(x)=x3+(a﹣1)x2+3x+1沒有極值點,則﹣2<a<4;
②集合M={1,2,zi},i為虛數單位,N={3,4},M∩N={4},則復數z=﹣4i;
③若函數f(x)= ![]() ﹣m有兩個零點,則m<
﹣m有兩個零點,則m< ![]() .
.
其中正確的是 .
【答案】②
【解析】解:①若f(x)=x3+(a﹣1)x2+3x+1,
則f′(x)=3x2+2(a﹣1)x+3,
若f(x)沒有極值點,則△≤0,
即4(a﹣1)2﹣36≤0,
即(a﹣1)2≤9,
得﹣3≤a﹣1≤3,則﹣2≤a≤4,故①錯誤,
②集合M={1,2,zi},i為虛數單位,N={3,4},M∩N={4},
則zi=4,則z= ![]() =﹣4i;故②正確,
=﹣4i;故②正確,
③若函數f(x)= ![]() ﹣m有兩個零點,則f(x)=
﹣m有兩個零點,則f(x)= ![]() ﹣m=0,即
﹣m=0,即 ![]() =m有兩個根,
=m有兩個根,
設g(x)= ![]() 則g′(x)=
則g′(x)= ![]() ,
,
由g′(x)>0得1﹣lnx>0得0<x<e,
g′(x)<0得1﹣lnx<0得x>e,
即當x=e時,函數f(x)取得極大值g(e)= ![]() =
= ![]() ,
,
當x>e時,g(x)= ![]() >0,
>0,
則若 ![]() =m有兩個根,
=m有兩個根,
則0<m< ![]() .故③錯誤,
.故③錯誤,
所以答案是:②
【考點精析】根據題目的已知條件,利用命題的真假判斷與應用的相關知識可以得到問題的答案,需要掌握兩個命題互為逆否命題,它們有相同的真假性;兩個命題為互逆命題或互否命題,它們的真假性沒有關系.


科目:高中數學 來源: 題型:
【題目】如圖是在豎直平面內的一個“通道游戲”.圖中豎直線段和斜線段都表示通道,并且在交點處相遇,若豎直線段有第一條的為第一層,有二條的為第二層,…,依此類推.現有一顆小彈子從第一層的通道里向下運動.若在通道的分叉處,小彈子以相同的概率落入每個通道,記小彈子落入第n層第m個豎直通道(從左至右)的概率為P(n,m).某研究性學習小組經探究發現小彈子落入第n層的第m個通道的次數服從二項分布,請你解決下列問題.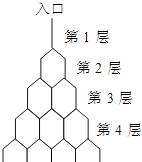
(1)求P(2,1),P(3,2)及P(4,2)的值,并猜想P(n,m)的表達式.(不必證明)
(2)設小彈子落入第6層第m個豎直通道得到分數為ξ,其中ξ= ![]() ,試求ξ的分布列及數學期望.
,試求ξ的分布列及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設p:實數x滿足x2﹣4ax+3a2<0,其中a<0,q:實數x滿足x2﹣x﹣6≤0或x2+2x﹣8>0,且非p是非q的必要不充分條件,則實數a的范圍是 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在統計學中,偏差是指個別測定值與測定的平均值之差,在成績統計中,我們把某個同學的某刻考試成績與該科班平均分的差叫某科偏差,班主任為了了解個別學生的偏科情況,對學生數學偏差![]() (單位:分)與物理偏差
(單位:分)與物理偏差![]() (單位:分)之間的關系進行偏差分析,決定從全班40位同學中隨機抽取一個容量為8的樣本進行分析,得到他們的兩科成績偏差數據如表:
(單位:分)之間的關系進行偏差分析,決定從全班40位同學中隨機抽取一個容量為8的樣本進行分析,得到他們的兩科成績偏差數據如表:

(1)已知![]() 與
與![]() 之間具有線性相關關系,求
之間具有線性相關關系,求![]() 關于
關于![]() 的線性回歸方程;
的線性回歸方程;
(2)若這次考試該班數學平均分為120分,物理平均分為92,試預測數學成績126分的同學的物理成績.
參考公式:  ,
, ![]()
參考數據: ![]() ,
, ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在直角坐標系![]() 中,直線
中,直線![]() 的傾斜角為
的傾斜角為![]() 且經過點
且經過點![]() ,以原點
,以原點![]() 為極點,以
為極點,以![]() 軸正半軸為極軸,與直角坐標系
軸正半軸為極軸,與直角坐標系![]() 取相同的長度單位,建立極坐標系,設曲線
取相同的長度單位,建立極坐標系,設曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)若直線![]() 與曲線
與曲線![]() 有公共點,求
有公共點,求![]() 的取值范圍;
的取值范圍;
(2)設![]() 為曲線
為曲線![]() 上任意一點,求
上任意一點,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知關于x的函數 ![]() .
.
(1)如果函數 ![]() ,求b、c;
,求b、c;
(2)設當x∈( ![]() ,3)時,函數y=f(x)﹣c(x+b)的圖象上任一點P處的切線斜率為k,若k≤2,求實數b的取值范圍.
,3)時,函數y=f(x)﹣c(x+b)的圖象上任一點P處的切線斜率為k,若k≤2,求實數b的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知△ABC的頂點A(5,1),AB邊上的中線CM所在直線方程為2x﹣y﹣5=0,∠B的平分線BN所在直線方程為x﹣2y﹣5=0.求:
(1)頂點B的坐標;
(2)直線BC的方程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com