
【題目】某種汽車,購車費用是10萬元,第一年維修費用是0.2萬元,以后逐年遞增0.2萬元,且每年的保險費、養路費、汽油費等約為0.9萬元.
(1)設這種汽車使用![]() 年(
年(![]() )的維修費用的和為
)的維修費用的和為![]() 萬元,求
萬元,求![]() 的表達式;
的表達式;
(2)這種汽車使用多少年時,它的年平均費用最小?
科目:高中數學 來源: 題型:
【題目】在四棱錐![]() 中,側面
中,側面![]() ⊥底面
⊥底面![]() ,底面
,底面![]() 為直角梯形,
為直角梯形,![]() //
//![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 為
為![]() 的中點.
的中點.

(Ⅰ)求證:PA//平面BEF;
(Ⅱ)若PC與AB所成角為![]() ,求
,求![]() 的長;
的長;
(Ⅲ)在(Ⅱ)的條件下,求二面角F-BE-A的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】狄利克雷是德國著名數學家,函數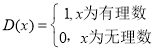 ,被稱為狄利克雷函數,下面給出關于狄利克雷函數
,被稱為狄利克雷函數,下面給出關于狄利克雷函數![]() 的五個結論:
的五個結論:
①若![]() 是無理數,則
是無理數,則![]() ;
;
②函數![]() 的值域是
的值域是![]() ;
;
③函數![]() 是偶函數;
是偶函數;
④若![]() 且
且![]() 為有理數,則
為有理數,則![]() 對任意的
對任意的![]() 恒成立;
恒成立;
⑤存在不同的三個點![]() ,使得
,使得![]() 為等邊三角形.
為等邊三角形.
其中正確結論的序號是___________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,圓
中,圓![]() 的參數方程為
的參數方程為![]() 為參數),直線
為參數),直線![]() 經過點
經過點![]() ,且傾斜角為
,且傾斜角為![]() .
.
(1)寫出直線![]() 的參數方程和圓
的參數方程和圓![]() 的標準方程;
的標準方程;
(2)設直線![]() 與圓
與圓![]() 相交于
相交于![]() 兩點,求
兩點,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列![]() 的前
的前![]() 項和為
項和為![]() ,滿足
,滿足![]() ,
,![]() ,數列
,數列![]() 滿足
滿足![]() ,
,![]() ,且
,且![]() .
.
(1)求數列![]() 的通項公式;
的通項公式;
(2)求證:數列![]() 是等差數列,求數列
是等差數列,求數列![]() 的通項公式;
的通項公式;
(3)若![]() ,數列
,數列![]() 的前
的前![]() 項和為
項和為![]() ,對任意的
,對任意的![]() ,都有
,都有![]() ,求實數
,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在等腰梯形ABCD中,AB=2DC=2,∠DAB=60°,E為AB的中點.將△ADE與△BEC分別沿ED、EC向上折起,使A、B重合于點P,則三棱錐PDCE的外接球的體積為( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】目前我國城市的空氣污染越來越嚴重,空氣質量指數![]() 一直居高不下,對人體的呼吸系統造成了嚴重的影響,現調查了某城市500名居民的工作場所和呼吸系統健康,得到
一直居高不下,對人體的呼吸系統造成了嚴重的影響,現調查了某城市500名居民的工作場所和呼吸系統健康,得到![]() 列聯表如下:
列聯表如下:
室外工作 | 室內工作 | 合計 | |
有呼吸系統疾病 | 150 | ||
無呼吸系統疾病 | 100 | ||
合計 | 200 |
(Ⅰ)請把![]() 列聯表補充完整;
列聯表補充完整;
(Ⅱ)你是否有95%的把握認為感染呼吸系統疾病與工作場所有關;
(Ⅲ)現采用分層抽樣從室內工作的居民中抽取一個容量為6的樣本,將該樣本看成一個總體,從中隨機抽取2人,求2人都有呼吸系統疾病的概率.
參考公式與臨界表:![]()
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com