
【題目】已知α∈![]() ,且sin
,且sin![]() +cos
+cos![]() =
=![]() .
.
(1)求cos α的值;
(2)若sin(α-β)=-![]() ,β∈
,β∈![]() ,求cos β的值.
,求cos β的值.
【答案】(1)![]() ;(2)
;(2)![]()
![]()
【解析】試題分析:(1)把已知條件平方可得sin α=![]() ,再由已知α∈
,再由已知α∈![]() ,可得cos α的值.
,可得cos α的值.
(2)由條件可得-![]() <α-β<
<α-β<![]() , cos(α-β)=
, cos(α-β)=![]() ,再根據cos β=cos[α-(α-β)],利用兩角和差的余弦公式,運算求得結果.
,再根據cos β=cos[α-(α-β)],利用兩角和差的余弦公式,運算求得結果.
試題解析: (1)已知sin![]() +cos
+cos![]() =
=![]() ,兩邊同時平方,
,兩邊同時平方,
得1+2sin![]() cos
cos![]() =
=![]() ,則sin α=
,則sin α=![]() .
.
又![]() <α<π,所以cos α=-
<α<π,所以cos α=-![]() =-
=-![]() .
.
(2)因為![]() <α<π,
<α<π, ![]() <β<π,所以-
<β<π,所以-![]() <α-β<
<α-β<![]() .
.
又sin(α-β)=-![]() ,所以cos(α-β)=
,所以cos(α-β)=![]() .
.
則cos β=cos[α-(α-β)]=cos αcos(α-β)+sin αsin(α-β)
=-![]() ×
×![]() +
+![]() ×
×![]() =-
=-![]() .
.
點睛: 本題考查的是三角函數式化簡中的給值求值問題,看“角”,這是最重要的一環,通過看角之間的區別和聯系,把角進行合理的拆分β=[α-(α-β),從而正確使用公式;由條件可得-![]() <α-β<
<α-β<![]() , cos(α-β)=
, cos(α-β)=![]() ,再根據cos β=cos[α-(α-β)],利用兩角和差的余弦公式,運算求得結果.
,再根據cos β=cos[α-(α-β)],利用兩角和差的余弦公式,運算求得結果.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】(2013·湖北高考)四名同學根據各自的樣本數據研究變量x,y之間的相關關系,并求得回歸直線方程,分別得到以下四個結論:
①y與x負相關且![]() =2.347x-6.423;
=2.347x-6.423;
②y與x負相關且![]() =-3.476x+5.648;
=-3.476x+5.648;
③y與x正相關且![]() =5.437x+8.493;
=5.437x+8.493;
④y與x正相關且![]() =-4.326x-4.578.
=-4.326x-4.578.
其中一定不正確的結論的序號是( )
A. ①② B. ②③ C. ③④ D. ①④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,在棱長為2cm的正方體ABCD﹣A1B1C1D1中,A1B1的中點是P,過點A1作出與截面PBC1平行的截面,簡單證明截面形狀,并求該截面的面積.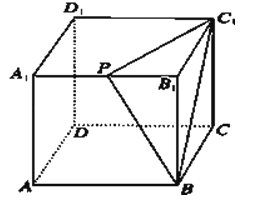
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某醫學院讀書協會欲研究晝夜溫差大小與患感冒人數多少之間的關系,該協會分別到氣象局與某醫院抄錄了1至6月份每月10號的晝夜溫差情況與因患感冒而就診的人數,得到如圖所示的頻率分布直方圖.該協會確定的研究方案是:先從這六組數據中選取2組,用剩下的4組數據求線性回歸方程,再用被選取的2組數據進行檢驗.

(Ⅰ)已知選取的是1月至6月的兩組數據,請根據2至5月份的數據,求出就診人數![]() 關于晝夜溫差
關于晝夜溫差![]() 的線性回歸方程;
的線性回歸方程;
(Ⅱ)若由線性回歸方程得到的估計數據與所選出的檢驗數據的誤差均不超過2人,則認為得到的線性回歸方程是理想的,試問(Ⅰ)中該協會所得線性回歸方程是否理想?
參考公式:回歸直線的方程![]() ,
,
其中 ,
, ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】給出40個數:1,2,4,7,11,16,…,要計算這40個數的和,如圖給出了該問題的程序框圖,那么框圖①處和執行框②處可分別填入( )
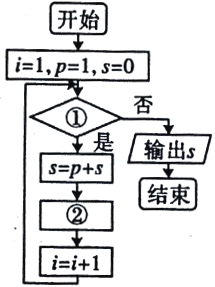
A. ![]() ;
; ![]() B.
B. ![]() ;
; ![]()
C. ![]() ;
; ![]() D.
D. ![]() ;
; ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
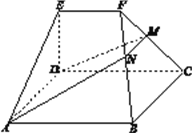
【題目】如圖,在幾何體![]() 中,底面
中,底面![]() 為矩形,
為矩形, ![]() ,
, ![]() .點
.點![]() 在棱
在棱![]() 上,平面
上,平面![]() 與棱
與棱![]() 交于點
交于點![]() .
.
(Ⅰ)求證: ![]() ;
;
(Ⅱ)求證:平面![]() 平面
平面![]() ;
;
(Ⅲ)若![]() ,
, ![]() ,
, ![]() ,平面
,平面![]() 平面
平面![]() ,求二面角
,求二面角![]() 的大小.
的大小.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com