Question

【題目】已知復數滿足，的虛部為，且在復平面內對應的點在第二象限.

（1）求復數；

（2）若復數滿足，求在復平面內對應的點的集合構成圖形的面積.

Answer 1

【答案】（1）；（2）

【解析】

（1）設出復數，利用已知列出方程組，求解可得復數； （2）把復數代入，利用復數代數形式的乘除運算化簡，由復數求模公式計算，由復數滿足，由復數的幾何意義得出在復平面內對應的點的集合構成圖形是什么，從而計算出對應面積.

(1)設z=x+yi(x,y∈R),則z2=x2-y2+2xyi,

由|z|=,z2的虛部為-2,且z在復平面內對應的點在第二象限,

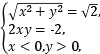得解得

∴z=-1+i.

(2)由(1)知,z=-1+i,

∴====-+i,

∴==,

∴復數ω滿足|ω-1|≤.

由復數的幾何意義,得

ω在復平面內對應的點的集合構成的圖形是以(1,0)為圓心,為半徑的圓面,

∴其面積為π·=.