
【題目】火電廠、核電站的循環水自然通風冷卻塔是一種大型薄殼型構筑物。建在水源不十分充足的地區的電廠,為了節約用水,需建造一個循環冷卻水系統,以使得冷卻器中排出的熱水在其中冷卻后可重復使用,大型電廠采用的冷卻構筑物多為雙曲線型冷卻塔.此類冷卻塔多用于內陸缺水電站,其高度一般為75~150米,底邊直徑65~120米. 雙曲線型冷卻塔比水池式冷卻構筑物占地面積小,布置緊湊,水量損失小,且冷卻效果不受風力影響;它比機力通風冷卻塔維護簡便,節約電能;但體形高大,施工復雜,造價較高.(以上知識來自百度,下面題設條件只是為了適合高中知識水平,其中不符合實際處請忽略.)

(1)如圖為一座高100米的雙曲線冷卻塔外殼的簡化三視圖(忽略壁厚),其底面直徑大于上底直徑,已知其外殼主視圖與左視圖中的曲線均為雙曲線,高度為100![]() ,俯視圖為三個同心圓,其半徑分別40
,俯視圖為三個同心圓,其半徑分別40![]() ,
,![]()
![]() ,30
,30![]() ,試根據上述尺寸計算視圖中該雙曲線的標準方程(
,試根據上述尺寸計算視圖中該雙曲線的標準方程(![]() 為長度單位米);
為長度單位米);

(2)試利用課本中推導球體積的方法,利用圓柱和一個倒放的圓錐,計算封閉曲線:![]() ,
,![]() ,繞
,繞![]() 軸旋轉形成的旋轉體的體積多少?(用
軸旋轉形成的旋轉體的體積多少?(用![]() 表示).(用積分計算不得分)現已知雙曲線冷卻塔是一個薄殼結構,為計算方便設其內壁所在曲線也為雙曲線,其壁最厚為0.4
表示).(用積分計算不得分)現已知雙曲線冷卻塔是一個薄殼結構,為計算方便設其內壁所在曲線也為雙曲線,其壁最厚為0.4![]() (底部),最薄處厚度為0.3
(底部),最薄處厚度為0.3![]() (喉部,即左右頂點處),試計算該冷卻塔內殼所在的雙曲線標準方程是?并計算本題中的雙曲線冷卻塔的建筑體積(內外殼之間)大約是多少
(喉部,即左右頂點處),試計算該冷卻塔內殼所在的雙曲線標準方程是?并計算本題中的雙曲線冷卻塔的建筑體積(內外殼之間)大約是多少![]() ;(計算時
;(計算時![]() 取3.14159,保留到個位即可)
取3.14159,保留到個位即可)

(3)冷卻塔體型巨大,造價相應高昂,本題只考慮地面以上部分的施工費用(建筑人工和輔助機械)的計算,鋼筋土石等建筑材料費用和和其它設備等施工費用不在本題計算范圍內.超高建筑的施工(含人工輔助機械等)費用隨著高度的增加而增加,現已知:距離地面高度30米(含30米)內的建筑,每立方米的施工費用平均為:400元/立方米;30米到40米(含40米)每立方米的施工費用為800元/立方米;40米以上,平均高度每增加1米,每立方米的施工費用增加100元.試計算建造本題中冷卻塔的施工費用(精確到萬元).
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ,
,![]() ,
,![]() ;(3)
;(3)![]() 萬元.
萬元.
【解析】
(1)由最窄處距離可求得![]() ;根據
;根據![]() 時,
時,![]() ;
;![]() 時,
時,![]() ,可構造方程求得
,可構造方程求得![]() ,從而得到雙曲線方程;(2)首先求得雙曲線旋轉體的體積和內層雙曲線方程,計算得到體積差的函數關系式,分別代入
,從而得到雙曲線方程;(2)首先求得雙曲線旋轉體的體積和內層雙曲線方程,計算得到體積差的函數關系式,分別代入![]() 和
和![]() 可求得體積差,加和得到所求體積;(3)由(2)可推得高度
可求得體積差,加和得到所求體積;(3)由(2)可推得高度![]() 時的幾何體體積;將在高度
時的幾何體體積;將在高度![]() 米以內的薄殼體積的建筑費用分為高度
米以內的薄殼體積的建筑費用分為高度![]() 米以內和高度在
米以內和高度在![]() 米之間兩類分別計算;設超過
米之間兩類分別計算;設超過![]() 米部分,每高
米部分,每高![]() 米的環形建筑物的體積構成數列
米的環形建筑物的體積構成數列![]() ,其相應的每立方米的施工費用對應為等差數列
,其相應的每立方米的施工費用對應為等差數列![]() ,易得
,易得![]() 通項公式;由雙曲線對稱性可知
通項公式;由雙曲線對稱性可知![]() ,進而可計算出此部分對應的建筑費用;綜合三部分的費用即可得到結果.
,進而可計算出此部分對應的建筑費用;綜合三部分的費用即可得到結果.
(1)![]() 最窄處即雙曲線兩頂點間
最窄處即雙曲線兩頂點間 ![]()
設雙曲線的標準方程為:![]()
由題意知:當![]() (地面半徑)時對應
(地面半徑)時對應![]() 的值是
的值是![]() ;當
;當![]() 時,
時,![]() 的值為
的值為![]()
![]() ,解得:
,解得:![]()
![]() 雙曲線的標準方程是
雙曲線的標準方程是![]() ,
,![]()
(2)高為![]() 的雙曲線旋轉體的體積是:
的雙曲線旋轉體的體積是:![]()
其旋轉體相當于一個底面半徑為![]() ,高為
,高為![]() 的圓柱與底面半徑為
的圓柱與底面半徑為![]() ,高為
,高為![]() 倒立圓錐的體積之和.
倒立圓錐的體積之和.
計算內層雙曲線方程為:![]()
![]() 高為
高為![]() 時雙曲線旋轉體的體積差為:
時雙曲線旋轉體的體積差為: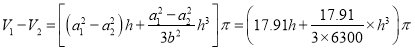
當![]() 與
與![]() 時,計算上述體積差,分別為
時,計算上述體積差,分別為![]() ,
,![]() ,合計約為
,合計約為![]() 立方米
立方米
![]() 冷卻塔的建筑體積約為
冷卻塔的建筑體積約為![]() 立方米
立方米
(3)由(2)知高為![]() 的雙曲線冷卻塔殼體體積為
的雙曲線冷卻塔殼體體積為![]() 立方米
立方米
![]() 立方米
立方米
![]() 當高度
當高度![]() 時,其幾何體體積為:
時,其幾何體體積為:![]()
于是在高度![]() 米以內的薄殼體積的建筑費用:
米以內的薄殼體積的建筑費用:
第一部分,高度![]() 米以內的體積:
米以內的體積:![]()
![]() 相應施工費用為:
相應施工費用為:![]() (元)
(元)
第二部分,高度在![]() 米之間的部分體積
米之間的部分體積![]()
![]() 相應施工費用為:
相應施工費用為:![]() (元)
(元)
設超過![]() 米部分,每高
米部分,每高![]() 米的環形建筑物的體積構成數列
米的環形建筑物的體積構成數列![]() ,其相應的每立方米的施工費用對應為等差數列
,其相應的每立方米的施工費用對應為等差數列![]()
![]()
注意到雙曲線的對稱性,本題中的冷卻塔喉部在高度![]() 米處,其上方
米處,其上方![]() 米,下方
米,下方![]() 處恰為高度
處恰為高度![]() 米處,于是
米處,于是![]()
又數列![]() 是等差數列
是等差數列 ![]()
![]() 這部分費用為:
這部分費用為:
![]()
![]()
其中![]() 為(2)中
為(2)中![]() 時殼體的體積,其值約為
時殼體的體積,其值約為![]()
![]() 這部分施工費用約為
這部分施工費用約為![]() (元)
(元)
綜上,本題中所求的施工總費用![]() 元,約
元,約![]() 萬元
萬元


科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
:![]() 的一個頂點為
的一個頂點為![]() ,且焦距為
,且焦距為![]() ,直線
,直線![]() 交橢圓
交橢圓![]() 于
于![]() 、
、![]() 兩點(點
兩點(點![]() 、
、![]() 與點
與點![]() 不重合),且滿足
不重合),且滿足![]() .
.
(1)求橢圓的標準方程;
(2)![]() 為坐標原點,若點
為坐標原點,若點![]() 滿足
滿足![]() ,求直線
,求直線![]() 的斜率的取值范圍.
的斜率的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知圓錐底面半徑![]() ,
,![]() 為底面圓圓心,點Q為半圓弧
為底面圓圓心,點Q為半圓弧![]() 的中點,點
的中點,點![]() 為母線
為母線![]() 的中點,
的中點,![]() 與
與![]() 所成的角為
所成的角為![]() ,求:
,求:

(1)圓錐的側面積;
(2)![]() 兩點在圓錐面上的最短距離.
兩點在圓錐面上的最短距離.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】說明下述命題是否可以看成判定定理或性質定理,如果可以,說出其中涉及的充分條件或必要條件:
(1)形如![]() (
(![]() 是非零常數)的函數是二次函數;
是非零常數)的函數是二次函數;
(2)菱形的對角線互相垂直.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對于函數![]() ,若在定義域存在實數
,若在定義域存在實數![]() ,滿足
,滿足![]() ,則稱
,則稱![]() 為“局部奇函數”.
為“局部奇函數”.
(1)已知二次函數![]() ,試判斷
,試判斷![]() 是否為“局部奇函數”?并說明理由;
是否為“局部奇函數”?并說明理由;
(2)設![]() 是定義在
是定義在![]() 上的“局部奇函數”,求實數
上的“局部奇函數”,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知二次函數f(x)滿足f(x)=f(2-x),且f(1)=6,f(3)=2.
(1)求f(x)的解析式
(2)是否存在實數m,使得在[-1,3]上f(x)的圖象恒在直線y=2mx+1的上方?若存在,求m的取值范圍;若不存在,說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com