
【題目】如圖,在三棱柱![]() 中,四邊形
中,四邊形![]() 是菱形,四邊形
是菱形,四邊形![]() 是正方形,
是正方形,![]() ,
,![]() ,
,![]() ,點
,點![]() 為
為![]() 的中點.
的中點.
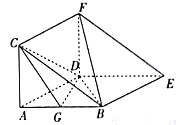
(1)求證:![]() 平面
平面![]() ;
;
(2)求平面![]() 與平面
與平面![]() 所成銳二面角的余弦值.
所成銳二面角的余弦值.
【答案】(1)見解析;(2)![]() .
.
【解析】
(1)(1)連接AF,與CD交于點H,連接GH,易得BF∥GH,從而得證;
(2)以D為原點,直線DG,DE,DF分別為x軸,y軸,z軸建立空間直角坐標系,通過求面BCD的一個法向量為![]() 和面BEF的一個法向量為
和面BEF的一個法向量為![]() ,利用
,利用![]() =
=![]() 即可得解.
即可得解.
(1)連接AF,與CD交于點H,連接GH,
則GH為△ABF的中位線,
所以BF∥GH,
又BF![]() 平面CDG,GH平面CDG,
平面CDG,GH平面CDG,
所以BF∥平面CDG.

(2)由題意可知,直線DG,DE,DF兩兩垂直,
以D為原點,直線DG,DE,DF分別為x軸,y軸,z軸建立如圖所示的空間直角坐標系,
則![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() .
.
設平面BCD的一個法向量為![]() =
=![]() ,則有
,則有 ,得
,得 ,
,
取![]() ,得,所以
,得,所以![]() =
=![]() ,
,
設平面BEF的一個法向量為![]() =
=![]() ,則有
,則有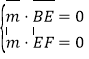 ,得
,得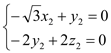 ,
,
取![]() ,得
,得![]() ,所以
,所以![]() =
=![]() ,
,
設平面BCD與平面BEF所成銳二面角為![]()
則![]() =
= ,
,
所以平面BCD與平面BEF所成銳二面角的余弦值為![]() .
.


科目:高中數學 來源: 題型:
【題目】某中學將要舉行校園歌手大賽,現有4男3女參加,需要安排他們的出場順序.(結果用數字作答)
(1)如果3個女生都不相鄰,那么有多少種不同的出場順序?
(2)如果女生甲在女生乙的前面(可以不相鄰),那么有多少種不同的出場順序?
(3)如果3位女生都相鄰,且女生甲不在第一個出場,那么有多少種不同的出場順序?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,以坐標原點
中,以坐標原點![]() 為極點,以
為極點,以![]() 軸正半軸為極軸建立極坐標系,已知曲線
軸正半軸為極軸建立極坐標系,已知曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)若兩條互相垂直的直線都經過原點(兩條直線與坐標軸都不重合)且與曲線![]() 分別交于點
分別交于點![]() (異于原點),且
(異于原點),且![]() ,求這兩條直線的直角坐標方程.
,求這兩條直線的直角坐標方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某學校共有教職工900人,分成三個批次進行繼續教育培訓,在三個批次中男、女教職工人數如下表所示. 已知在全體教職工中隨機抽取1名,抽到第二批次中女教職工的概率是0.16 .

(1)求![]() 的值;
的值;
(2)現用分層抽樣的方法在全體教職工中抽取54名做培訓效果的調查, 問應在第三批次中抽取教職工多少名?
(3)已知![]() ,求第三批次中女教職工比男教職工多的概率.
,求第三批次中女教職工比男教職工多的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】法國有個名人叫做布萊爾·帕斯卡,他認識兩個賭徒,這兩個賭徒向他提出一個問題,他們說,他們下賭金之后,約定誰先贏滿5局,誰就獲得全部賭金700法郎,賭了半天,甲贏了4局,乙贏了3局,時間很晚了,他們都不想再賭下去了.假設每局兩賭徒輸贏的概率各占![]() ,每局輸贏相互獨立,那么這700法郎如何分配比較合理( )
,每局輸贏相互獨立,那么這700法郎如何分配比較合理( )
A.甲400法郎,乙300法郎B.甲500法郎,乙200法郎
C.甲525法郎,乙175法郎D.甲350法郎,乙350法郎
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,一張矩形白紙![]() ,
,![]() ,
,![]() 分別為
分別為![]() 的中點,現分別將
的中點,現分別將![]() 沿
沿![]() 折起,且點
折起,且點![]() ,
,![]() 在平面
在平面![]() 同側,則下列命題正確的是______(寫出所有正確命題的序號)
同側,則下列命題正確的是______(寫出所有正確命題的序號)

①當平面![]() //平面
//平面![]() 時,
時,![]() //平面
//平面![]() ;
;
②當平面![]() //平面
//平面![]() 時,
時,![]() //
//![]() ;
;
③當![]() ,
,![]() 重合于點
重合于點![]() 時,
時,![]() ;
;
④當![]() ,
,![]() 重合于點
重合于點![]() 時,三棱錐
時,三棱錐![]() 的外接球的表面積為
的外接球的表面積為![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com