
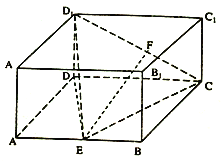
【題目】長方體![]() 中,
中, ![]() ,
, ![]() 分別是
分別是![]() ,
, ![]() 的中點,
的中點, ![]() ,
, ![]() .
.
(Ⅰ)求證: ![]() 平面
平面![]() ;
;
(Ⅱ)求證:平面![]() 平面
平面![]() ;
;
(Ⅲ)在線段![]() 上是否存在一點
上是否存在一點![]() ,使得二面角
,使得二面角![]() 為
為![]() ,若存在,求
,若存在,求![]() 的值;若不存在,說明理由.
的值;若不存在,說明理由.
【答案】(Ⅰ)見解析; (Ⅱ)見解析;(Ⅲ)線段![]() 上存在一點
上存在一點![]() ,使得二面角
,使得二面角![]() 為
為![]() ,且
,且![]() .
.
【解析】試題分析:(Ⅰ)要證![]() 與平面
與平面![]() 平行,就是要證
平行,就是要證![]() 與平面內的一條直線平行,由長方體的特征,過
與平面內的一條直線平行,由長方體的特征,過![]() 作
作![]() 交
交![]() 于點
于點![]() ,可證
,可證![]() 與
與![]() 平行且相等,從而得
平行且相等,從而得![]() ,得線面平行;
,得線面平行;
(Ⅱ)要證面面垂直,首先在矩形![]() 中,由已知可得
中,由已知可得![]() ,因此再由長方體一性質有
,因此再由長方體一性質有![]() ,從而得
,從而得![]() 與平面
與平面![]() 垂直,于是有面面垂直;
垂直,于是有面面垂直;
(Ⅲ)以![]() 為原點,
為原點, ![]() 、
、![]() 、
、![]() 所在直線為
所在直線為![]() 軸、
軸、![]() 軸、
軸、![]() 軸建立坐標系,寫出各點坐標,設
軸建立坐標系,寫出各點坐標,設![]() (
(![]() ),從而得
),從而得![]() ,求出二面角
,求出二面角![]() 的兩個面的法向量,由法向量的夾角余弦的絕對值為
的兩個面的法向量,由法向量的夾角余弦的絕對值為![]() 可求得
可求得![]() 值,從而確定Q點是否存在.
值,從而確定Q點是否存在.
試題解析:
(Ⅰ)證明:過![]() 作
作![]() 交
交![]() 于
于![]() ,連接
,連接![]() .
.
∵![]() 是
是![]() 的中點,∴
的中點,∴![]() ,
, ![]() ,
,
又∵![]() 是
是![]() 中點,∴
中點,∴![]() ,
, ![]() ,
,
∴![]() ,
, ![]() ,
, ![]() 是平行四邊形,
是平行四邊形,
∴![]() ,
,
又![]() 在平面
在平面![]() 內,∴
內,∴![]() 平面
平面![]() .
.
(Ⅱ)證明:∵![]() 平面
平面![]() ,
, ![]() 在平面
在平面![]() 內,
內,
∴![]() ,
,
在矩形![]() 中,
中, ![]() ,
,
∴![]() ,
,
∴![]() 是直角三角形,∴
是直角三角形,∴![]() ,
,
∴![]() 平面
平面![]() ,
,
∵![]() 在平面
在平面![]() 內,∴平面
內,∴平面![]() 平面
平面![]() .
.
(Ⅲ)解:以![]() 為原點,
為原點, ![]() 、
、![]() 、
、![]() 所在直線為
所在直線為![]() 軸、
軸、![]() 軸、
軸、![]() 軸建立坐標系,則
軸建立坐標系,則![]() ,
, ![]() ,
, ![]() .
.
平面![]() 的法向量為
的法向量為![]() ,
,
設![]() ,(
,( ![]() ),則
),則![]() ,
,
設平面![]() 的法向量為
的法向量為![]() ,
,
則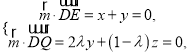 令
令![]() ,則
,則![]() ,
,
∵二面角![]() 為
為![]() ,
,
∴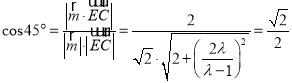 ,
,
由于![]() ,∴
,∴![]() ,
,
∴線段![]() 上存在一點
上存在一點![]() ,使得二面角
,使得二面角![]() 為
為![]() ,且
,且![]() .
.


科目:高中數學 來源: 題型:
【題目】已知![]() 是拋物線
是拋物線![]() 與圓
與圓![]() 在第一象限的公共點,其中圓心
在第一象限的公共點,其中圓心![]() ,點
,點![]() 到
到![]() 的焦點
的焦點![]() 的距離與
的距離與![]() 的半徑相等,
的半徑相等, ![]() 上一動點到其準線與到點
上一動點到其準線與到點![]() 的距離之和的最小值等于
的距離之和的最小值等于![]() 的直徑,
的直徑, ![]() 為坐標原點,則直線
為坐標原點,則直線![]() 被圓
被圓![]() 所截得的弦長為( )
所截得的弦長為( )
A. 2 B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某汽車站每天均有3輛開往省城的分為上、中、下等級的客車,某天袁先生準備在該汽車站乘車前往省城辦事,但他不知道客車的車況,也不知道發車順序.為了盡可能乘上上等車,他采取如下策略:先放過一輛,如果第二輛比第一輛好則上第二輛,否則上第三輛.則他乘上上等車的概率為________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知某運動員每次投籃命中的概率低于![]() ,現采用隨機模擬的方法估計該運動員三次投籃恰有兩次命中的概率:先由計算器產生0到9之間取整數值的隨機數,指定1,2,3,4表示命中,5,6,7,8,9,0表示不命中;再以每三個隨機數為一組,代表三次投籃的結果,經隨機模擬產生了如下20組隨機數:
,現采用隨機模擬的方法估計該運動員三次投籃恰有兩次命中的概率:先由計算器產生0到9之間取整數值的隨機數,指定1,2,3,4表示命中,5,6,7,8,9,0表示不命中;再以每三個隨機數為一組,代表三次投籃的結果,經隨機模擬產生了如下20組隨機數:
907 966 191 925 271 932 812 458 569 683
431 257 393 027 556 488 730 113 537 989
據此估計,該運動員三次投籃恰有兩次命中的概率為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校高三數學競賽初賽考試后,對部分考生的成績進行統計(考生成績均不低于90分,滿分150分),將成績按如下方式分成六組,若第四、五、六組的人數依次成等差數列,且第六組有4人.

(1)請補充完整頻率分布直方圖,并估計這組數據的平均數M;
(2)現根據初賽成績從第四組和第六組中任意選2人,記他們的成績分別為![]() .若
.若![]() ,則稱此二人為“黃金幫扶組”.試求選出的二人為“黃金幫扶組”的概率
,則稱此二人為“黃金幫扶組”.試求選出的二人為“黃金幫扶組”的概率![]() ;
;
(3)以此樣本的頻率當做概率,現隨機在這所有考生中選出3名學生,求成績不低于120分的人數![]() 的分布列及期望.
的分布列及期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一個盒子里裝有三張卡片,分別標記有數字1,2,3,這三張卡片除標記的數字外完全相同.隨機有放回地抽取3次,每次抽取1張,將抽取的卡片上的數字依次記為a,b,c.求:
(1)“抽取的卡片上的數字滿足a+b=c”的概率;
(2)“抽取的卡片上的數字a,b,c不完全相同”的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2015年7月9日21時15分,臺風“蓮花”在我國廣東省陸豐市甲東鎮沿海登陸,給當地人民造成了巨大的財產損失,適逢暑假,小張調查了當地某小區的100戶居民由于臺風造成的經濟損失,將收集的數據分成![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 五組,并作出如下頻率分布直方圖(圖1):
五組,并作出如下頻率分布直方圖(圖1):
(Ⅰ)臺風后居委會號召小區居民為臺風重災區捐款,小張調查的100戶居民捐款情況如右下表格,在圖2表格空白處填寫正確數字,并說明是否有![]() 以上的把握認為捐款數額多于或少于500元和自身經濟損失是否到4000元有關?
以上的把握認為捐款數額多于或少于500元和自身經濟損失是否到4000元有關?


(Ⅱ)將上述調查所得到的頻率視為概率. 現在從該地區大量受災居民中,采用隨機抽樣方法每次抽取1戶居民,抽取3次,記被抽取的3戶居民中自身經濟損失超過4000元的人數為![]() . 若每次抽取的結果是相互獨立的,求
. 若每次抽取的結果是相互獨立的,求![]() 的分布列,期望
的分布列,期望![]() 和方差
和方差![]() .
.
附:臨界值表
| 0.10 | 0.05 | 0.025 |
| 2.706 | 3.841 | 5.024 |
隨機量變

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲、乙二人做射擊游戲,甲、乙射擊擊中與否是相互獨立事件.規則如下:若射擊一次擊中,則原射擊人繼續射擊;若射擊一次不中,就由對方接替射擊.已知甲、乙二人射擊一次擊中的概率均為![]() ,且第一次由甲開始射擊.①求前3次射擊中甲恰好擊中2次的概率____________;②求第4次由甲射擊的概率________.
,且第一次由甲開始射擊.①求前3次射擊中甲恰好擊中2次的概率____________;②求第4次由甲射擊的概率________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com