
【題目】設函數f(x)= ![]() x2+ax﹣lnx(a∈R). (Ⅰ)當a=1時,求函數f(x)的極值;
x2+ax﹣lnx(a∈R). (Ⅰ)當a=1時,求函數f(x)的極值;
(Ⅱ)當a>1時,討論函數f(x)的單調性;
(Ⅲ)若對任意a∈(3,4)及任意x1 , x2∈[1,2],恒有 ![]() m+ln2>|f(x1)﹣f(x2)|成立,求實數m的取值范圍.
m+ln2>|f(x1)﹣f(x2)|成立,求實數m的取值范圍.
【答案】解:(Ⅰ)函數的定義域為(0,+∞) 當a=1時,f(x)=x﹣lnx,則f′(x)= ![]()
令f′(x)>0,可得x<0或x>1,∵x>0,∴x>1;
令f′(x)<0,可得0<x<1,∵x>0,∴0<x<1;
∴x=1時,函數f(x)取得極小值為1;
(Ⅱ)f′(x)= 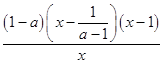
當 ![]() ,即a=2時,
,即a=2時, ![]() ,f(x)在(0,+∞)上是減函數;
,f(x)在(0,+∞)上是減函數;
當 ![]() ,即a>2時,令f′(x)<0,得
,即a>2時,令f′(x)<0,得 ![]() 或x>1;令f′(x)>0,得
或x>1;令f′(x)>0,得 ![]()
當 ![]() ,即1<a<2時,令f′(x)<0,得0<x<1或x>
,即1<a<2時,令f′(x)<0,得0<x<1或x> ![]() ;令f′(x)>0,得
;令f′(x)>0,得 ![]()
綜上,當a=2時,f(x)在定義域上是減函數;
當a>2時,f(x)在(0, ![]() )和(1,+∞)上單調遞減,在(
)和(1,+∞)上單調遞減,在( ![]() ,1)上單調遞增;
,1)上單調遞增;
當1<a<2時,f(x)在(0,1)和( ![]() ,+∞)上單調遞減,在(1,
,+∞)上單調遞減,在(1, ![]() )上單調遞增;
)上單調遞增;
(Ⅲ)由(Ⅱ)知,當a∈(3,4)時,f(x)在[1,2]上單調遞減
∴當x=1時,f(x)有最大值,當x=2時,f(x)有最小值
∴ ![]()
∴對任意a∈(3,4),恒有 ![]()
∴m> ![]()
構造函數 ![]() ,則
,則 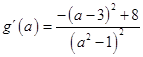
∵a∈(3,4),∴ 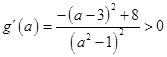
∴函數 ![]() 在(3,4)上單調增
在(3,4)上單調增
∴g(a)∈(0, ![]() )
)
∴m≥ ![]() .
.
【解析】(Ⅰ)確定函數的定義域,利用導數的正負,確定函數的單調性,從而可求函數的極值;(Ⅱ)求導函數f′(x)= ![]() ,分類討論,利用導數的正負,確定函數的單調性; (Ⅲ)由(Ⅱ)知,當a∈(3,4)時,f(x)在[1,2]上單調遞減,從而可得
,分類討論,利用導數的正負,確定函數的單調性; (Ⅲ)由(Ⅱ)知,當a∈(3,4)時,f(x)在[1,2]上單調遞減,從而可得 ![]() 對任意a∈(3,4),恒有
對任意a∈(3,4),恒有 ![]() ,等價于m>
,等價于m> ![]() ,求出右邊函數的值域,即可求得結論.
,求出右邊函數的值域,即可求得結論.


科目:高中數學 來源: 題型:
【題目】甲、乙兩人在相同條件下各打靶10次,每次打靶所得的環數如圖所示.
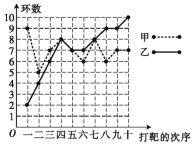
填寫下表,請從下列角度對這次結果進行分析.
命中9環及以上的次數 | 平均數 | 中位數 | 方差 | |
甲 | ||||
乙 |
(1)命中9環及以上的次數(分析誰的成績好些);
(2)平均數和中位數(分析誰的成績好些);
(3)方差(分析誰的成績更穩定);
(4)折線圖上兩人射擊命中環數的走勢(分析誰更有潛力).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為 ,(
,(![]() 為參數),圓
為參數),圓![]() 的標準方程為
的標準方程為![]() .以坐標原點為極點,
.以坐標原點為極點, ![]() 軸正半軸為極軸建立極坐標系.
軸正半軸為極軸建立極坐標系.
(1)求直線![]() 和圓
和圓![]() 的極坐標方程;
的極坐標方程;
(2)若射線![]() 與的交點為
與的交點為![]() ,與圓
,與圓![]() 的交點為
的交點為![]() ,且點
,且點![]() 恰好為線段
恰好為線段![]() 的中點,求
的中點,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在正整數數列中,由1開始依次按如下規則,將某些整數染成紅色,先染1;再染3個偶數2,4,6;再染6后面最鄰近的5個連續奇數7,9,11,13,15;再染15后面最鄰近的7個連續偶數16,18,20,22,24,26,28;再染此后最鄰近的9個連續奇數29,31,…,45;按此規則一直染下去,得到一紅色子數列:1,2,4,6,7,9,11,13,15,16,……,則在這個紅色子數列中,由1開始的第2019個數是( )
A. 3972 B. 3974 C. 3991 D. 3993
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某單位安排![]() 位員工在春節期間大年初一到初七值班,每人值班
位員工在春節期間大年初一到初七值班,每人值班![]() 天,若
天,若![]() 位員工中的甲、乙排在相鄰的兩天,丙不排在初一,丁不排在初七,則不同的安排方案共有_______
位員工中的甲、乙排在相鄰的兩天,丙不排在初一,丁不排在初七,則不同的安排方案共有_______
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為比較甲、乙兩地某月14時的氣溫狀況,隨機選取該月中的5天,將這5天中14時的氣溫數據(單位:℃)制成如圖所示的莖葉圖.考慮以下結論:
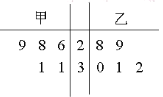
①甲地該月14時的平均氣溫低于乙地該月14時的平均氣溫;
②甲地該月14時的平均氣溫高于乙地該月14時的平均氣溫;
③甲地該月14時的平均氣溫的標準差小于乙地該月14時的氣溫的標準差;
④甲地該月14時的平均氣溫的標準差大于乙地該月14時的氣溫的標準差.
其中根據莖葉圖能得到的統計結論的標號為 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數g(x)=a﹣x2( ![]() ≤x≤e,e為自然對數的底數)與h(x)=2lnx的圖象上存在關于x軸對稱的點,則實數a的取值范圍是( )
≤x≤e,e為自然對數的底數)與h(x)=2lnx的圖象上存在關于x軸對稱的點,則實數a的取值范圍是( )
A.[1, ![]() +2]
+2]
B.[1,e2﹣2]
C.[ ![]() +2,e2﹣2]
+2,e2﹣2]
D.[e2﹣2,+∞)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一支車隊有![]() 輛車,某天依次出發執行運輸任務。第一輛車于下午
輛車,某天依次出發執行運輸任務。第一輛車于下午![]() 時出發,第二輛車于下午
時出發,第二輛車于下午![]() 時
時![]() 分出發,第三輛車于下午
分出發,第三輛車于下午![]() 時
時![]() 分出發,以此類推。假設所有的司機都連續開車,并都在下午
分出發,以此類推。假設所有的司機都連續開車,并都在下午![]() 時停下來休息.
時停下來休息.
到下午![]() 時,最后一輛車行駛了多長時間?
時,最后一輛車行駛了多長時間?
如果每輛車的行駛速度都是![]() ,這個車隊當天一共行駛了多少
,這個車隊當天一共行駛了多少![]() ?
?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知直線![]() :
:![]() (
(![]() 為參數),曲線
為參數),曲線![]() :
:![]() (
(![]() 為參數).
為參數).
(1)設![]() 與
與![]() 相交于
相交于![]() ,
,![]() 兩點,求
兩點,求![]() 的值;
的值;
(2)若把曲線![]() 上各點的橫坐標壓縮為原來的
上各點的橫坐標壓縮為原來的![]() ,縱坐標壓縮為原來的
,縱坐標壓縮為原來的![]() ,得到曲線
,得到曲線![]() ,設點
,設點![]() 是曲線
是曲線![]() 上的一個動點,求它到直線
上的一個動點,求它到直線![]() 的距離的最小值.
的距離的最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com