
【題目】如圖,四棱錐P﹣ABCD的底面ABCD是正方形,PA⊥底面ABCD,E,F分別是AC,PB的中點(diǎn).
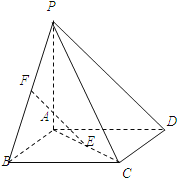
(1)證明:EF∥平面PCD;
(2)求證:面PBD⊥面PAC;
(3)若PA=AB,求PD與平面PAC所成角的大小.
【答案】(1)證明見詳解(2)證明見詳解(3)![]()
【解析】
(1)作![]() 中點(diǎn)
中點(diǎn)![]() ,
,![]() 中點(diǎn)
中點(diǎn)![]() ,連接
,連接![]() ,通過求證四邊形
,通過求證四邊形![]() 為平行四邊形進(jìn)而求證;
為平行四邊形進(jìn)而求證;
(2)可結(jié)合正方形性質(zhì)和線面垂直性質(zhì)設(shè)法證明![]() ,進(jìn)而求證;
,進(jìn)而求證;
(3)連接![]() ,可證
,可證![]() 即為PD與平面PAC所成角的大小,通過幾何關(guān)系即可求解;
即為PD與平面PAC所成角的大小,通過幾何關(guān)系即可求解;
(1)如圖,作![]() 中點(diǎn)
中點(diǎn)![]() ,
,![]() 中點(diǎn)
中點(diǎn)![]() ,連接
,連接![]() ,
,
![]() 分別為
分別為![]() 中點(diǎn),
中點(diǎn),![]() 且
且![]() ,同理
,同理![]() 且
且![]() ,又底面
,又底面![]() 為正方形,
為正方形,![]() ,
,
![]() ,
,![]() 為平行四邊形,
為平行四邊形,![]() ,又
,又![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,![]() 平面
平面![]()
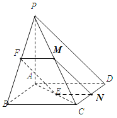
(2)連接![]() ,
,![]() 底面
底面![]() 為正方形,
為正方形,![]() ,又
,又![]() PA⊥底面ABCD,
PA⊥底面ABCD,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() 平面
平面![]() ,又因
,又因![]() 平面
平面![]() ,
,![]() 平面PBD⊥平面PAC;
平面PBD⊥平面PAC;
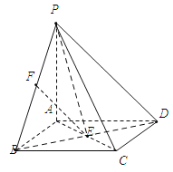
(3)連接![]() ,由(2)可知,
,由(2)可知,![]() 平面
平面![]() ,也即
,也即![]() 平面
平面![]() ,則
,則![]() 即為PD與平面PAC所成角的大小,設(shè)底面正方形邊長(zhǎng)為
即為PD與平面PAC所成角的大小,設(shè)底面正方形邊長(zhǎng)為![]() ,
,
則![]() ,
,![]() ,所以
,所以![]()


 學(xué)而優(yōu)銜接教材南京大學(xué)出版社系列答案
學(xué)而優(yōu)銜接教材南京大學(xué)出版社系列答案 小學(xué)課堂作業(yè)系列答案
小學(xué)課堂作業(yè)系列答案 金博士一點(diǎn)全通系列答案
金博士一點(diǎn)全通系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓C:![]() 1(a
1(a![]() b
b![]() 0)的左、右焦點(diǎn)分別為F1,F2,點(diǎn)P為橢圓C上不與左右頂點(diǎn)重合的動(dòng)點(diǎn),設(shè)I,G分別為△PF1F2的內(nèi)心和重心.當(dāng)直線IG的傾斜角不隨著點(diǎn)P的運(yùn)動(dòng)而變化時(shí),橢圓C的離心率為_____.
0)的左、右焦點(diǎn)分別為F1,F2,點(diǎn)P為橢圓C上不與左右頂點(diǎn)重合的動(dòng)點(diǎn),設(shè)I,G分別為△PF1F2的內(nèi)心和重心.當(dāng)直線IG的傾斜角不隨著點(diǎn)P的運(yùn)動(dòng)而變化時(shí),橢圓C的離心率為_____.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]()
(1)求![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(2)過點(diǎn)![]() 存在幾條直線與曲線
存在幾條直線與曲線![]() 相切,并說明理由;
相切,并說明理由;
(3)若![]() 對(duì)任意
對(duì)任意![]() 恒成立,求實(shí)數(shù)
恒成立,求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
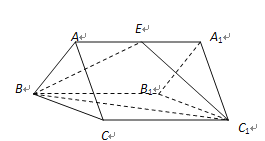
【題目】如圖:三棱柱![]() 的所有棱長(zhǎng)均相等,
的所有棱長(zhǎng)均相等,![]() ,
,![]() 為
為![]() 的中點(diǎn).
的中點(diǎn).
(1)求證:平面![]() ⊥平面
⊥平面![]() ;
;
(2)求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】今年1月至2月由新型冠狀病毒引起的肺炎病例陡然增多,為了嚴(yán)控疫情傳播,做好重點(diǎn)人群的預(yù)防工作,某地區(qū)共統(tǒng)計(jì)返鄉(xiāng)人員![]() 人,其中
人,其中![]() 歲及以上的共有
歲及以上的共有![]() 人.這
人.這![]() 人中確診的有
人中確診的有![]() 名,其中
名,其中![]() 歲以下的人占
歲以下的人占![]() .
.
(1)請(qǐng)將下面的列聯(lián)表補(bǔ)充完整,并判斷是否有![]() %的把握認(rèn)為是否確診患新冠肺炎與年齡有關(guān);
%的把握認(rèn)為是否確診患新冠肺炎與年齡有關(guān);
確診患新冠肺炎 | 未確診患新冠肺炎 | 合計(jì) | |
50歲及以上 | 40 | ||
50歲以下 | |||
合計(jì) | 10 | 100 |
(2)為了研究新型冠狀病毒的傳染源和傳播方式,從![]() 名確診人員中隨機(jī)抽出
名確診人員中隨機(jī)抽出![]() 人繼續(xù)進(jìn)行血清的研究,
人繼續(xù)進(jìn)行血清的研究,![]() 表示被抽取的
表示被抽取的![]() 人中
人中![]() 歲以下的人數(shù),求
歲以下的人數(shù),求![]() 的分布列以及數(shù)學(xué)期望.
的分布列以及數(shù)學(xué)期望.
參考表:
| 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
參考公式: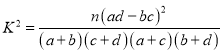 ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】橢圓規(guī)是畫橢圓的一種工具,如圖1所示,在十字形滑槽上各有一個(gè)活動(dòng)滑標(biāo)![]() ,
,![]() ,有一根旋桿將兩個(gè)滑標(biāo)連成一體,
,有一根旋桿將兩個(gè)滑標(biāo)連成一體,![]() ,
,![]() 為旋桿上的一點(diǎn),且在
為旋桿上的一點(diǎn),且在![]() ,
,![]() 兩點(diǎn)之間,且
兩點(diǎn)之間,且![]() ,當(dāng)滑標(biāo)
,當(dāng)滑標(biāo)![]() 在滑槽
在滑槽![]() 內(nèi)作往復(fù)運(yùn)動(dòng),滑標(biāo)
內(nèi)作往復(fù)運(yùn)動(dòng),滑標(biāo)![]() 在滑槽
在滑槽![]() 內(nèi)隨之運(yùn)動(dòng)時(shí),將筆尖放置于
內(nèi)隨之運(yùn)動(dòng)時(shí),將筆尖放置于![]() 處可畫出橢圓,記該橢圓為
處可畫出橢圓,記該橢圓為![]() .如圖2所示,設(shè)
.如圖2所示,設(shè)![]() 與
與![]() 交于點(diǎn)
交于點(diǎn)![]() ,以
,以![]() 所在的直線為
所在的直線為![]() 軸,以
軸,以![]() 所在的直線為
所在的直線為![]() 軸,建立平面直角坐標(biāo)系.
軸,建立平面直角坐標(biāo)系.

(1)求橢圓![]() 的方程;
的方程;
(2)設(shè)![]() ,
,![]() 是橢圓
是橢圓![]() 的左右頂點(diǎn),點(diǎn)
的左右頂點(diǎn),點(diǎn)![]() 為直線
為直線![]() 上的動(dòng)點(diǎn),直線
上的動(dòng)點(diǎn),直線![]() ,
,![]() 分別交橢圓于
分別交橢圓于![]() ,
,![]() 兩點(diǎn),求四邊形
兩點(diǎn),求四邊形![]() 面積為
面積為![]() ,求點(diǎn)
,求點(diǎn)![]() 的坐標(biāo).
的坐標(biāo).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在三棱錐A﹣BCD中,點(diǎn)E在BD上,EA=EB=EC=ED,BD![]() CD,△ACD為正三角形,點(diǎn)M,N分別在AE,CD上運(yùn)動(dòng)(不含端點(diǎn)),且AM=CN,則當(dāng)四面體C﹣EMN的體積取得最大值
CD,△ACD為正三角形,點(diǎn)M,N分別在AE,CD上運(yùn)動(dòng)(不含端點(diǎn)),且AM=CN,則當(dāng)四面體C﹣EMN的體積取得最大值![]() 時(shí),三棱錐A﹣BCD的外接球的表面積為_____.
時(shí),三棱錐A﹣BCD的外接球的表面積為_____.

查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
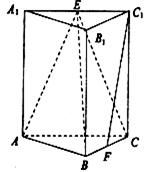
【題目】如圖,在三棱錐![]() 中,側(cè)棱垂直于底面,
中,側(cè)棱垂直于底面, ![]() 分別是
分別是![]() 的中點(diǎn).
的中點(diǎn).
(1)求證: 平面![]() 平面
平面![]() ;
;
(2)求證: ![]() 平面
平面![]() ;
;
(3)求三棱錐![]() 體積.
體積.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】一對(duì)夫婦為了給他們的獨(dú)生孩子支付將來上大學(xué)的費(fèi)用,從孩子一周歲生日開始,每年到銀行儲(chǔ)蓄![]() 元一年定期,若年利率為
元一年定期,若年利率為![]() 保持不變,且每年到期時(shí)存款(含利息)自動(dòng)轉(zhuǎn)為新的一年定期,當(dāng)孩子18歲生日時(shí)不再存入,將所有存款(含利息)全部取回,則取回的錢的總數(shù)為
保持不變,且每年到期時(shí)存款(含利息)自動(dòng)轉(zhuǎn)為新的一年定期,當(dāng)孩子18歲生日時(shí)不再存入,將所有存款(含利息)全部取回,則取回的錢的總數(shù)為![]()
![]()
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com