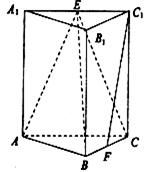
【題目】如圖，在三棱錐
中，側棱垂直于底面， 
分別是
的中點．
（1）求證: 平面
平面
；
（2）求證: 
平面
；
（3）求三棱錐
體積．
【答案】（1）證明見解析；（2）證明見解析；（3）
．
【解析】試題分析：（1）由直線與平面垂直證明直線與平行的垂直；（2）證明直線與平面平行；（3）求三棱錐的體積就用體積公式.
（1）在三棱柱
中， 
底面ABC，所以
AB，
又因為AB⊥BC，所以AB⊥平面
，因為AB
平面
，所以平面
平面
.
（2）取AB中點G，連結EG，FG，
因為E，F分別是
、
的中點，所以FG∥AC，且FG=
AC，
因為AC∥
，且AC=
，所以FG∥
，且FG= 
，
所以四邊形
為平行四邊形，所以
EG，
又因為EG
平面ABE， 
平面ABE，
所以
平面
.
（3）因為
=AC=2，BC=1，AB⊥BC，所以AB=
，
所以三棱錐
的體積為： 
=
=
.
科目：高中數學 來源： 題型：
【題目】在△ABC中，角A、B、C所對的邊分別為a、b、c，| 
|=5，20a 
+15b 
+12c = 
， 
=2 
，則 
的值為（ ）
A.
B.﹣ 
C.﹣
D.﹣8
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
在
處有極值，且其圖像在
處的切線與直線
平行.
(I).求函數的單調區間；
(II).求函數的極大值與極小值的差；
(III).若
時，
恒成立，求實數
的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】下列說法：①殘差可用來判斷模型擬合的效果;
②設有一個回歸方程
，變量x增加一個單位時，y平均增加5個單位；
③線性回歸方程
必過
；
④在一個2×2列聯表中，由計算得
=13.079，則有99%的把握確認這兩個變量間有關系（其中
）；
其中錯誤的個數是（ ）
A. 0 B. 1 C. 2 D. 3.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知數列{an}的各項均為正數，滿足a1=1，ak+1﹣ak=ai ． （i≤k，k=1，2，3，…，n﹣1）
（1）求證： 
；
（2）若{an}是等比數列，求數列{an}的通項公式；
（3）設數列{an}的前n項和為Sn ， 求證： 
．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設a＜1，集合A={x∈R|x＞0}，B={x∈R|2x2﹣3（1+a）x+6a＞0}，D=A∩B．
（1）求集合D（用區間表示）；
（2）求函數f（x）=2x3﹣3（1+a）x2+6ax在D內的極值點．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
