
【題目】如圖,半徑為4m的水輪繞著圓心O逆時針做勻速圓周運動,每分鐘轉動4圈,水輪圓心O距離水面2m,如果當水輪上點P從離開水面的時刻(P0)開始計算時間. 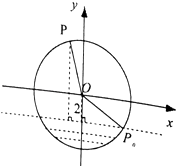
(1)將點P距離水面的高度y(m)與時間t(s)滿足的函數關系;
(2)求點P第一次到達最高點需要的時間.
【答案】
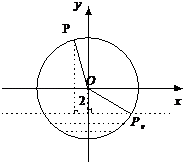
(1)解:以O為原點建立如圖所示的直角坐標系.
由于水輪繞著圓心O做勻速圓周運動,可設點P到水面的距離y(m)與時間t(s)滿足函數關系 ![]() ,
,
∵水輪每分鐘旋轉4圈,
∴ ![]() .
.
∴ ![]() .
.
∵水輪半徑為4 m,
∴A=4.
∴ ![]() .
.
當t=0時,y=0.
∴ ![]() .
.
∴ ![]() .
.
(2)解:由于最高點距離水面的距離為6,
∴ ![]() .
.
∴ ![]() .
.
∴ ![]() .
.
∴t=5+15k(k∈Z).
∴當k=0時,即t=5(s)時,點P第一次達到最高點.
【解析】(1)設點P到水面的距離y(m)與時間t(s)滿足函數關系 ![]() ,利用周期求得ω,當t=0時,y=0,進而求得φ的值,則函數的表達式可得.(2)根據正弦函數的圖象和性質可得t=5+15k(k∈Z)即當k=0時,即t=5(s)時,點P第一次達到最高點.
,利用周期求得ω,當t=0時,y=0,進而求得φ的值,則函數的表達式可得.(2)根據正弦函數的圖象和性質可得t=5+15k(k∈Z)即當k=0時,即t=5(s)時,點P第一次達到最高點.


科目:高中數學 來源: 題型:
【題目】已知函數f(x)=2sinxcosx+2cos(x+ ![]() )cos(x﹣
)cos(x﹣ ![]() ).
).
(1)求f(x)的單調遞減區間;
(2)設α∈(0,π),f( ![]() )=
)= ![]() ,求sinα的值.
,求sinα的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,
, ![]() .
.
(Ⅰ)當![]() 時,求函數
時,求函數![]() 的極值;
的極值;
(Ⅱ)當![]() 時,討論函數
時,討論函數![]() 單調性;
單調性;
(Ⅲ)是否存在實數![]() ,對任意的
,對任意的![]() ,
, ![]() ,且
,且![]() ,有
,有![]() 恒成立?若存在,求出
恒成立?若存在,求出![]() 的取值范圍;若不存在,說明理由.
的取值范圍;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】記a=logsin1cos1,b=logsin1tan1,c=logcos1sin1,d=logcos1tan1,則四個數的大小關系是( )
A.a<c<b<d
B.c<d<a<b
C.b<d<c<a
D.d<b<a<c
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《九章算術》是我國古代數學成就的杰出代表.其中《方田》章給出計算弧田面積所用的經驗公式為:弧田面積= ![]() (弦×矢+矢2).弧田,由圓弧和其所對弦所圍成.公式中“弦”指圓弧對弦長,“矢”等于半徑長與圓心到弦的距離之差,按照上述經驗公式計算所得弧田面積與實際面積之間存在誤差.現有圓心角為
(弦×矢+矢2).弧田,由圓弧和其所對弦所圍成.公式中“弦”指圓弧對弦長,“矢”等于半徑長與圓心到弦的距離之差,按照上述經驗公式計算所得弧田面積與實際面積之間存在誤差.現有圓心角為 ![]() π,弦長等于9米的弧田.按照《九章算術》中弧田面積的經驗公式計算所得弧田面積與實際面積的差為 .
π,弦長等于9米的弧田.按照《九章算術》中弧田面積的經驗公式計算所得弧田面積與實際面積的差為 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,
, ![]() ,其中
,其中![]() ,
, ![]() ,
, ![]() 為自然對數的底數.
為自然對數的底數.
(Ⅰ)若![]() 和
和![]() 在區間
在區間![]() 內具有相同的單調性,求實數
內具有相同的單調性,求實數![]() 的取值范圍;
的取值范圍;
(Ⅱ)若![]() ,且函數
,且函數![]() 的最小值為
的最小值為![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=sin(ωx+φ)﹣b(ω>0,0<φ<π)的圖象兩相鄰對稱軸之間的距離是 ![]() ,若將f(x)的圖象先向右平移
,若將f(x)的圖象先向右平移 ![]() 個單位,再向上平移
個單位,再向上平移 ![]() 個單位,所得函數g(x)為奇函數.
個單位,所得函數g(x)為奇函數.
(1)求f(x)的解析式;
(2)求f(x)的對稱軸及單調區間;
(3)若對任意x∈[0, ![]() ],f2(x)﹣(2+m)f(x)+2+m≤0恒成立,求實數m的取值范圍.
],f2(x)﹣(2+m)f(x)+2+m≤0恒成立,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一個社會調查機構就某地居民的月收入調查了10 000人,并根據所得數據畫了樣本的頻率分布直方圖(如圖).為了分析居民的收入與年齡、學歷、職業等方面的關系,要從這10 000人中再用分層抽樣方法抽出80人作進一步調查,則在[1 500,2 000)(元)月收入段應抽出( )人. 
A.15
B.16
C.17
D.18
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】國內,某知名連接店分店開張營業期間,在固定的時間段內消費達到一定標準的顧客可進行一次抽獎活動,隨著抽獎的有效展開,參與抽獎活動的人數越來越多,該分店經理對開業前7天參加抽獎活動的人數進行統計, ![]() 表示開業第
表示開業第![]() 天參加抽獎活動的人數,得到統計表格如下:
天參加抽獎活動的人數,得到統計表格如下:

經過進一步的統計分析,發現![]() 與
與![]() 具有線性相關關系.
具有線性相關關系.
(1)如從這7天中隨便機抽取兩天,求至少有1天參加抽獎人數超過10天的概率;
(2)根據上表給出的數據,用最小二乘法,求出![]() 與
與![]() 的線性回歸方程
的線性回歸方程![]() ,并估計若該活動持續10天,共有多少名顧客參加抽獎.
,并估計若該活動持續10天,共有多少名顧客參加抽獎.
參考公式: 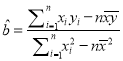 ,
, ![]() ,
, ![]() ,
, ![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com