
【題目】已知![]() 是數列
是數列![]() 的前n項和,
的前n項和,![]() ,且
,且![]() .
.
(1)求數列![]() 的通項公式;
的通項公式;
(2)對于正整數![]() ,已知
,已知![]() 成等差數列,求正整數
成等差數列,求正整數![]() 的值;
的值;
(3)設數列![]() 前n項和是
前n項和是![]() ,且滿足:對任意的正整數n,都有等式
,且滿足:對任意的正整數n,都有等式![]() 成立.求滿足等式
成立.求滿足等式![]() 的所有正整數n.
的所有正整數n.
【答案】(1)![]() (2)
(2)![]() (3)1和3.
(3)1和3.
【解析】試題分析:(1)先根據和項與通項關系得項之間遞推關系,再根據等比數列定義判斷,最后根據等比數列通項公式求結果,(2)根據等差數列化簡得![]() ,再根據正整數限制條件以及指數性質確定不定方程正整數解,(3)先根據定義求數列
,再根據正整數限制條件以及指數性質確定不定方程正整數解,(3)先根據定義求數列![]() 通項公式,再根據等差數列求和公式求
通項公式,再根據等差數列求和公式求![]() ,根據數列相鄰項關系確定
,根據數列相鄰項關系確定![]() 遞減,最后根據單調性求正整數解.
遞減,最后根據單調性求正整數解.
試題解析:(1)由![]()
![]() 得
得![]() ,兩式作差得
,兩式作差得![]() ,即
,即![]()
![]() .
.
![]() ,
,![]() ,所以
,所以![]()
![]() ,
,![]() ,則
,則![]()
![]() ,所以數列
,所以數列![]() 是首項為
是首項為![]() 公比為
公比為![]() 的等比數列,所以
的等比數列,所以![]()
![]() ;
;
(2)由題意![]() ,即
,即![]() ,
,
所以![]() ,其中
,其中![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,
![]() ,所以
,所以![]() ,
,![]() ,
,![]() ;
;
(3)由![]()
![]()
![]() 得,
得,
![]()
![]()
![]() ,
,
![]()
![]()
![]() ,
,
![]()
![]() ,
,
所以![]()
![]() ,即
,即![]() ,
,
所以![]()
![]() ,
,
又因為![]() ,得
,得![]() ,所以
,所以![]()
![]() ,
,
從而![]()
![]()
![]() ,
,![]() ,
,
當![]() 時
時![]() ;當
;當![]() 時
時![]() ;當
;當![]() 時
時![]() ;
;
下面證明:對任意正整數![]() 都有
都有![]() ,
,
![]()
![]()
![]()
![]()
![]() ,
,
當![]() 時,
時,![]()
![]() ,即
,即![]() ,
,
所以當![]() 時,
時,![]() 遞減,所以對任意正整數
遞減,所以對任意正整數![]() 都有
都有![]() ;
;
綜上可得,滿足等式![]() 的正整數
的正整數![]() 的值為
的值為![]() 和
和![]() .
.


科目:高中數學 來源: 題型:
【題目】十八屆五中全會公報指出:努力促進人口均衡發展,堅持計劃生育的基本國策,完善人口發展戰略,全面實施一對夫婦可生育兩個孩子的政策,提高生殖健康、婦幼保健、托幼等公共服務水平.為了解適齡公務員對放開生育二胎政策的態度,某部門隨機調查了100位30到40歲的公務員,得到情況如下表:
男公務員 | 女公務員 | |
生二胎 | 40 | 20 |
不生二胎 | 20 | 20 |
(1)是否有95%以上的把握認為“生二胎與性別有關”,并說明理由;
(2)把以上頻率當概率,若從社會上隨機抽取3位30到40歲的男公務員,記其中生二胎的人數為X,求隨機變量X的分布列,數學期望.
附:K2= ![]()
P(K2≥k0) | 0.050 | 0.010 | 0.001 |
k0 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xoy中,圓的參數方程為 ![]() (φ為參數),以坐標原點O為極點,x軸的正半軸為極軸的極坐標系中,直線l的極坐標方程為
(φ為參數),以坐標原點O為極點,x軸的正半軸為極軸的極坐標系中,直線l的極坐標方程為 ![]() .
.
(1)將圓的參數方程化為普通方程,在化為極坐標方程;
(2)若點P在直線l上,當點P到圓的距離最小時,求點P的極坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某班級50名學生的考試分數x分布在區間[50,100)內,設分數x的分布頻率是f(x)且f(x)= 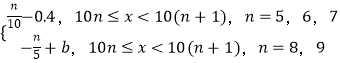 ,考試成績采用“5分制”,規定:考試分數在[50,60)內的成績記為1分,考試分數在[60,70)內的成績記為2分,考試分數在[70,80)內的成績記為3分,考試分數在[80,90)內的成績記為4分,考試分數在[90,100)內的成績記為5分.用分層抽樣的方法,現在從成績在1分,2分及3分的人中用分層抽樣隨機抽出6人,再從這6人中抽出3人,記這3人的成績之和為ξ(將頻率視為概率).
,考試成績采用“5分制”,規定:考試分數在[50,60)內的成績記為1分,考試分數在[60,70)內的成績記為2分,考試分數在[70,80)內的成績記為3分,考試分數在[80,90)內的成績記為4分,考試分數在[90,100)內的成績記為5分.用分層抽樣的方法,現在從成績在1分,2分及3分的人中用分層抽樣隨機抽出6人,再從這6人中抽出3人,記這3人的成績之和為ξ(將頻率視為概率).
(1)求b的值,并估計班級的考試平均分數;
(2)求P(ξ=7);
(3)求ξ的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)= ![]() sin(x+
sin(x+ ![]() )﹣
)﹣ ![]() cos(x+
cos(x+ ![]() ),若存在x1 , x2 , x3 , …,xn滿足0≤x1<x2<x3<…<xn≤6π,且|f(x1)﹣f(x2)|+|f(x2)﹣f(x3)|+…
),若存在x1 , x2 , x3 , …,xn滿足0≤x1<x2<x3<…<xn≤6π,且|f(x1)﹣f(x2)|+|f(x2)﹣f(x3)|+… ![]() ,則n的最小值為( )
,則n的最小值為( )
A.6
B.10
C.8
D.12
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知等比數列{an}的第2項、第5項分別為二項式(2x+1)5展開式的第5項、第2項的系數.
(1)求數列{an}的通項公式;
(2)記數列{an}的前n項和為Sn , 若存在實數λ,使 ![]() 恒成立,求實數λ的取值范圍.
恒成立,求實數λ的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某市司法部門為了宣傳《憲法》舉辦法律知識問答活動,隨機對該市![]() 歲的人群抽取一個容量為
歲的人群抽取一個容量為![]() 的樣本,并將樣本數據分成五組:
的樣本,并將樣本數據分成五組:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,再將其按從左到右的順序分別編號為第1組,第2組,…,第5組,繪制了樣本的頻率分布直方圖;并對回答問題情況進行統計后,結果如下表所示.
,再將其按從左到右的順序分別編號為第1組,第2組,…,第5組,繪制了樣本的頻率分布直方圖;并對回答問題情況進行統計后,結果如下表所示.
組號 | 分組 | 回答正確的人數 | 回答正確的人數占本組的比例 |
第1組 |
|
|
|
第2組 |
|
|
|
第3組 |
|
|
|
第4組 |
|
|
|
第5組 |
|
|
|
(1)分別求出![]() ,
,![]() 的值;
的值;
(2)從第![]() ,
,![]() ,
,![]() 組回答正確的人中用分層抽樣方法抽取
組回答正確的人中用分層抽樣方法抽取![]() 人,則第
人,則第![]() ,
,![]() ,
,![]() 組每組應各抽取多少人?
組每組應各抽取多少人?
(3)在(2)的前提下,決定在所抽取的![]() 人中隨機抽取
人中隨機抽取![]() 人頒發幸運獎,求:所抽取的人中第2組至少有
人頒發幸運獎,求:所抽取的人中第2組至少有![]() 人獲得幸運獎概率.
人獲得幸運獎概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com