【題目】已知
時，函數
有極值
（1）求實數
的值；
（2）若方程
有3個實數根，求實數
的取值范圍。
【答案】（1）
；（2）
【解析】
（1）先求導數，根據f（1）＝-2，f′（1）＝0列出方程求出a，b；
（2）由（1）所求解析式可得f′（x），利用導數可得f（x）的單調區間及極值，根據f（x）的圖象的大致形狀即可求得k的范圍；
（1）因為
，所以f′（x）＝3ax2+b．
又因為當x＝1時，f（x）的極值為-2，所以
，
解得a＝1，b＝-3．
（2）由（1）可得
，f′（x）＝3x2-3＝3（x+1）（x﹣1），
令f′（x）＝0，得x＝±1，
當x＜﹣1或x＞1時f′（x）＞0，f(x)單調遞增，當﹣1＜x＜1時，f′（x）＜0，f(x)單調遞減；
所以當x＝﹣1時f（x）取得極大值，f（﹣1）
，當x＝1時f（x）取得極小值，f（1）
，大致圖像如圖：
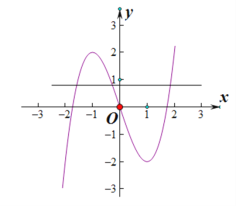
要使方程f（x）＝k有3個解，只需
k
．
故實數k的取值范圍為（-2，2）．
科目：高中數學 來源： 題型：
【題目】已知函數
(
>0)的部分圖象如圖所示，A，B分別是這部分圖象上的最高點、最低點，
為坐標原點，若
·
＝0，
則下列結論：①函數
是周期為4的奇函數；②函數
是周期為4的偶函數；③函數
的最大值是
；④函數向左平移
個單位后得到的函數圖象關于原點對稱；其中錯誤命題的個數是（ ）
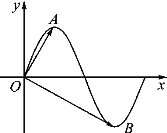
A.3B.2C.1D.0
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某企業有甲、乙兩套設備生產同一種產品，為了檢測兩套設備的生產質量情況，隨機從兩套設備生產的大量產品中各抽取了50件產品作為樣本，檢測一項質量指標值，若該項質量指標值落在
內，則為合格品，否則為不合格品. 表1是甲套設備的樣本的頻數分布表，圖1是乙套設備的樣本的頻率分布直方圖.
表1：甲套設備的樣本的頻數分布表
質量指標值 | [95,100) | [100,105) | [105,110) | [110,115) | [115,120) | [120,125] |
頻數 | 1 | 4 | 19 | 20 | 5 | 1 |
圖1：乙套設備的樣本的頻率分布直方圖
（1）填寫下面列聯表，并根據列聯表判斷是否有90%的把握認為該企業生產的這種產品的質量指標值與甲、乙兩套設備的選擇有關；
