
【題目】在平面直角坐標系中,橫、縱坐標均為整數的點叫做格點.若函數圖象恰好經過k個格點,則稱函數為k階格點函數.已知函數:
①y=sinx; ②y=cos(x+![]() ); ③y=ex-1; ④y=x2.
); ③y=ex-1; ④y=x2.
其中為一階格點函數的序號為 ( )
A. ①② B. ②③ C. ①③ D. ②④
【答案】C
【解析】對于①,注意到y=sinx的值域是[-1,1];當sinx=0時,x=kπ(k∈Z),此時相應的整數x=0;當sinx=±1時,x=kπ+![]() (k∈Z),此時沒有相應的整數x,因此函數y=sinx僅過唯一的整點(0,0),該函數是一階格點函數.同理可知,對于②,函數y=cos(x+
(k∈Z),此時沒有相應的整數x,因此函數y=sinx僅過唯一的整點(0,0),該函數是一階格點函數.同理可知,對于②,函數y=cos(x+![]() )不是一階格點函數.對于③,令y=ex-1=k(k∈Z)得ex=k+1>0,x=ln(k+1),僅當k=0時,x=0∈Z,因此函數y=ex-1是一階格點函數.對于④,注意到函數y=x2的圖象經過多個整點,如點(0,0),(1,1),因此函數y=x2不是一階格點函數.綜上所述知選C.
)不是一階格點函數.對于③,令y=ex-1=k(k∈Z)得ex=k+1>0,x=ln(k+1),僅當k=0時,x=0∈Z,因此函數y=ex-1是一階格點函數.對于④,注意到函數y=x2的圖象經過多個整點,如點(0,0),(1,1),因此函數y=x2不是一階格點函數.綜上所述知選C.


科目:高中數學 來源: 題型:
【題目】上半年產品產量與單位成本資料如下:
月份 | 產量/千件 | 單位成本/元 |
1 | 2 | 73 |
2 | 3 | 72 |
3 | 4 | 71 |
4 | 3 | 73 |
5 | 4 | 69 |
6 | 5 | 68 |
且已知產量x與單位成本y具有線性相關關系.
(1)求出回歸方程.
(2)指出產量每增加1 000件時,單位成本平均變動多少?
(3)假定產量為6 000件時,單位成本為多少元?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲、乙兩個籃球運動員互不影響地在同一位置投球,命中率分別為![]() 與
與![]() ,且乙投球3次均未命中的概率為
,且乙投球3次均未命中的概率為![]() ,甲投球未命中的概率恰是乙投球未命中的概率的2倍.
,甲投球未命中的概率恰是乙投球未命中的概率的2倍.
(Ⅰ)求乙投球的命中率![]() ;
;
(Ⅱ)若甲投球1次,乙投球2次,兩人共命中的次數記為![]() ,求
,求![]() 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】廠為了對新研發的一種產品進行合理定價,將該產品按事先擬定的價格進行試銷,得到如下數據:
單價x/元 | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
銷量y/件 | 90 | 84 | 83 | 80 | 75 | 68 |
(1)求線性回歸方程![]() =
=![]() x+
x+![]() ,其中
,其中![]() =-20,
=-20, ![]() =
=![]() -
-![]()
![]() .
.
(2)預計在今后的銷售中,銷量與單價仍然服從(1)中的關系,且該產品的成本是4元/件,為使工廠獲得最大利潤,該產品的單價應定為多少元?(利潤=銷售收入-成本)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在調查運動員是否服用過興奮劑的時候,給出兩個問題作答,無關緊要的問題是:“你的身份證號碼的尾數是奇數嗎?”敏感的問題是:“你服用過興奮劑嗎?”然后要求被調查的運動員擲一枚硬幣,如果出現正面,就回答第一個問題,否則回答第二個問題.由于回答哪一個問題只有被測試者自己知道,所以應答者一般樂意如實地回答問題.若我們把這種方法用于300個被調查的運動員,得到80個“是”的回答,則這群運動員中服用過興奮劑的百分率大約為_____.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 為直角梯形,
為直角梯形, ![]() ,
, ![]() ,平面
,平面![]() 平面
平面![]() ,
, ![]() 為
為![]() 的中點,
的中點, ![]() 是棱
是棱![]() 上的點,
上的點, ![]() ,
, ![]() ,
, ![]() .
.
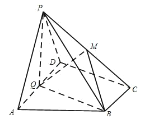
(1)求證:平面![]() 平面
平面![]() ;
;
(2)若二面角![]() 大小為
大小為![]() ,求線段
,求線段![]() 的長.
的長.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】現從某班的一次期末考試中,隨機的抽取了七位同學的數學(滿分150分)、物理(滿分110分)成績如下表所示,數學、物理成績分別用特征量![]() 表示,
表示,
特征量 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
t | 101 | 124 | 119 | 106 | 122 | 118 | 115 |
y | 74 | 83 | 87 | 75 | 85 | 87 | 83 |
求![]() 關于t的回歸方程;
關于t的回歸方程;
(2)利用(1)中的回歸方程,分析數學成績的變化對物理成績的影響,并估計該班某學生數學成績130分時,他的物理成績(精確到個位).
附:回歸方程![]() 中斜率和截距的最小二乘估計公式分別為:
中斜率和截距的最小二乘估計公式分別為:
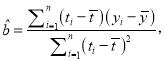
![]() .
. ![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com