
【題目】一個盒子中裝有4個形狀大小完全相同的球,球的編號分別為1,2,3,4.
(1)從盒子中不放回隨機抽取兩個球,求取出的球的編號之和不大于4的概率;
(2)先從盒子中隨機取一個球,該球的編號為![]() ,將球放回盒子中,然后再從盒子中隨機取一個球,該球的編號為
,將球放回盒子中,然后再從盒子中隨機取一個球,該球的編號為![]() ,求
,求![]() 的概率.
的概率.
【答案】(1)![]() (2)
(2)![]()
【解析】試題分析:(1)根據列舉法表示所有取到2個不同小球的組合情況,并計算其中兩個小球和不大于4的個數,相除即時概率;(2)列舉出所有![]() 的組合情況,并且計算其中滿足條件
的組合情況,并且計算其中滿足條件![]() 的個數,利用對立事件求概率,或是直接計算
的個數,利用對立事件求概率,或是直接計算![]() 的個數,并計算概率.
的個數,并計算概率.
試題解析:(1)從袋中隨機抽取兩個球,其一切可能的結果組成的基本事件有1和2,1和
3,1和4,2和3,2和4,3和4,共6個.
從袋中取出的球的編號之和不大于4的事件共有1和2,1和3兩個.
因此所求事件的概率p=![]()
(2)先從袋中隨機取一個球,記下編號為m,放回后,再從袋中隨機取一個球,記
下編號為n,其一切可能的結果(m,n)有:
(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4),
(3,1),(3,2),(3,3),(3,4),(4,1),(4,2),(4,3),(4,4),共16個.
又滿足條件![]() 的事件為(1,3),(1,4),(2,4),共3個,
的事件為(1,3),(1,4),(2,4),共3個,
滿足條件![]() 的事件的概率為
的事件的概率為![]() ,
,
所以條件![]() 的事件的概率為
的事件的概率為![]() .
.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】已知a=(5![]() cos x,cos x),b=(sin x,2cos x),設函數f(x)=a·b+|b|2+
cos x,cos x),b=(sin x,2cos x),設函數f(x)=a·b+|b|2+![]() .
.
(1) 求函數f (x)的最小正周期和對稱中心;
(2) 當![]() 時,求函數f(x)的值域;
時,求函數f(x)的值域;
(3) 該函數y=f (x)的圖象可由![]() 的圖象經過怎樣的變換得到?
的圖象經過怎樣的變換得到?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列說法:
①將一組數據中的每個數據都加上或減去同一個常數后,方差恒不變;
②設有一個回歸方程![]() ,變量x增加一個單位時,y平均增加5個單位;
,變量x增加一個單位時,y平均增加5個單位;
③線性回歸直線![]() 必過
必過![]() ;
;
④曲線上的點與該點的坐標之間具有相關關系;
⑤在一個2×2列聯表中,由計算得K2=13.079.則其兩個變量間有關系的可能性是90%.
其中錯誤的個數是( )
A. 1 B. 2
C. 3 D. 4
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】將邊長為1的正方形AA1O1O(及其內部)繞OO1旋轉一周形成圓柱,如圖, 弧AC 長為 ![]() ,弧A1B1 長為
,弧A1B1 長為 ![]() ,其中B1與C在平面AA1O1O的同側.
,其中B1與C在平面AA1O1O的同側. 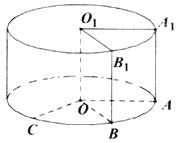
(1)求圓柱的體積與側面積;
(2)求異面直線O1B1與OC所成的角的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知某射擊運動員,每次擊中目標的概率都是![]() .現采用隨機模擬的方法估計該運動員射擊
.現采用隨機模擬的方法估計該運動員射擊![]() 次至少擊中
次至少擊中![]() 次的概率:先由計算器算出
次的概率:先由計算器算出![]() 到
到![]() 之間取整數值的隨機數,指定
之間取整數值的隨機數,指定![]() ,
,![]() 表示沒有擊中目標,
表示沒有擊中目標,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 表示擊中目標;因為射擊
表示擊中目標;因為射擊![]() 次,故以每
次,故以每![]() 個隨機數為一組,代表射擊
個隨機數為一組,代表射擊![]() 次的結果.經隨機模擬產生了如下
次的結果.經隨機模擬產生了如下![]() 組隨機數:
組隨機數:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
據此估計,該射擊運動員射擊![]() 次至少擊中
次至少擊中![]() 次的概率為( )
次的概率為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某商場經銷某商品,根據以往資料統計,顧客采用的付款期數X的分布列為
X | 1 | 2 | 3 | 4 | 5 |
P | 0.4 | 0.2 | 0.2 | 0.1 | 0.1 |
商場經銷一件該商品,采用1期付款,其利潤為200元;分2期或3期付款,其利潤為250元;分4期或5期付款,其利潤為300元.Y表示經銷一件該商品的利潤.
(1)求事件:“購買該商品的3位顧客中,至少有1位采用1期付款”的概率P(A);
(2)求Y的分布列及E(Y).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數f(x)=x﹣a(x+1)ln(x+1),(x>﹣1,a≥0)
(Ⅰ)求f(x)的單調區間;
(Ⅱ)當a=1時,若方程f(x)=t在 ![]() 上有兩個實數解,求實數t的取值范圍;
上有兩個實數解,求實數t的取值范圍;
(Ⅲ)證明:當m>n>0時,(1+m)n<(1+n)m .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com