
【題目】已知橢圓![]()
(1)求橢圓![]() 的標(biāo)準(zhǔn)方程和離心率;
的標(biāo)準(zhǔn)方程和離心率;
(2)是否存在過(guò)點(diǎn)![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 相交于
相交于![]() ,
,![]() 兩點(diǎn),且滿足
兩點(diǎn),且滿足![]() .若存在,求出直線
.若存在,求出直線![]() 的方程;若不存在,請(qǐng)說(shuō)明理由.
的方程;若不存在,請(qǐng)說(shuō)明理由.
【答案】(1)![]() ,
,![]() ;(2)存在,7x﹣
;(2)存在,7x﹣![]() +3
+3![]() =0或7x+
=0或7x+![]() ﹣3
﹣3![]() =0
=0
【解析】
(1)將橢圓方程化為標(biāo)準(zhǔn)方程,可得a,b,c,由離心率公式可得所求值;
(2)假設(shè)存在過(guò)點(diǎn)P(0,3)的直線l與橢圓C相交于A,B兩點(diǎn),且滿足![]() ,可設(shè)直線l的方程為x=m(y﹣3),聯(lián)立橢圓方程,消去x可得y的二次方程,運(yùn)用韋達(dá)定理和判別式大于0,再由向量共線的坐標(biāo)表示,化簡(jiǎn)整理解方程,即可判斷是否存在這樣的直線.
,可設(shè)直線l的方程為x=m(y﹣3),聯(lián)立橢圓方程,消去x可得y的二次方程,運(yùn)用韋達(dá)定理和判別式大于0,再由向量共線的坐標(biāo)表示,化簡(jiǎn)整理解方程,即可判斷是否存在這樣的直線.
(1)由![]() ,得
,得![]() ,進(jìn)而
,進(jìn)而![]() ,
,![]() ;
;
(2)假設(shè)存在過(guò)點(diǎn)P(0,3)的直線l與橢圓C相交于A,B兩點(diǎn),且滿足![]() ,
,
可設(shè)直線l的方程為x=m(y﹣3),聯(lián)立橢圓方程x2+2y2=4,
可得(2+m2)y2﹣6m2y+9m2﹣4=0,△=36m4﹣4(2+m2)(9m2﹣4)>0,即m2<![]() ,
,
設(shè)A(x1,y1),B(x2,y2),可得y1+y2=![]() ,y1y2=
,y1y2=![]() ,①
,①
由![]() ,可得(x2,y2﹣3)=2(x1,y1﹣3),即y2﹣3=2(y1﹣3),即y2=2y1﹣3,②
,可得(x2,y2﹣3)=2(x1,y1﹣3),即y2﹣3=2(y1﹣3),即y2=2y1﹣3,②
將②代入①可得3y1﹣3=![]() ,y1(2y1﹣3)=
,y1(2y1﹣3)=![]() ,
,
消去y1,可得![]()
![]() =
=![]() ,解得m2=
,解得m2=![]()
![]() ,所以
,所以![]() ,
,
故存在這樣的直線l,且方程為7x﹣![]() y+3
y+3![]() =0或7x+
=0或7x+![]() y﹣3
y﹣3![]() =0.
=0.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】函數(shù)![]() 的部分圖象如圖,M是圖象的一個(gè)最低點(diǎn),圖象與x軸的一個(gè)交點(diǎn)的坐標(biāo)為
的部分圖象如圖,M是圖象的一個(gè)最低點(diǎn),圖象與x軸的一個(gè)交點(diǎn)的坐標(biāo)為![]() ,與y軸的交點(diǎn)坐標(biāo)為
,與y軸的交點(diǎn)坐標(biāo)為![]() .
.
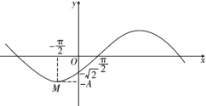
(1)求A,![]() ,
,![]() 的值;
的值;
(2)若關(guān)于x的方程![]() 在
在![]() 上有一解,求實(shí)數(shù)m的取值范圍.
上有一解,求實(shí)數(shù)m的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)![]() 是偶函數(shù)
是偶函數(shù)
(1)求k的值;
(2)若函數(shù)![]() 的圖象與直線
的圖象與直線![]() 沒(méi)有交點(diǎn),求b的取值范圍;
沒(méi)有交點(diǎn),求b的取值范圍;
(3)設(shè)![]() ,若函數(shù)
,若函數(shù)![]() 與
與![]() 的圖象有且只有一個(gè)公共點(diǎn),求實(shí)數(shù)
的圖象有且只有一個(gè)公共點(diǎn),求實(shí)數(shù)![]() 的取值范圍
的取值范圍
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在海岸線l一側(cè)P處有一個(gè)美麗的小島,某旅游公司為方便登島游客,在l上設(shè)立了M,N兩個(gè)報(bào)名接待點(diǎn),P,M,N三點(diǎn)滿足任意兩點(diǎn)間的距離為![]() 公司擬按以下思路運(yùn)作:先將M,N兩處游客分別乘車(chē)集中到MN之間的中轉(zhuǎn)點(diǎn)Q處
公司擬按以下思路運(yùn)作:先將M,N兩處游客分別乘車(chē)集中到MN之間的中轉(zhuǎn)點(diǎn)Q處![]() 點(diǎn)Q異于M,N兩點(diǎn)
點(diǎn)Q異于M,N兩點(diǎn)![]() ,然后乘同一艘游輪由Q處前往P島
,然后乘同一艘游輪由Q處前往P島![]() 據(jù)統(tǒng)計(jì),每批游客報(bào)名接待點(diǎn)M處需發(fā)車(chē)2輛,N處需發(fā)車(chē)4輛,每輛汽車(chē)的運(yùn)費(fèi)為20元
據(jù)統(tǒng)計(jì),每批游客報(bào)名接待點(diǎn)M處需發(fā)車(chē)2輛,N處需發(fā)車(chē)4輛,每輛汽車(chē)的運(yùn)費(fèi)為20元![]() ,游輪的運(yùn)費(fèi)為120元
,游輪的運(yùn)費(fèi)為120元![]() 設(shè)
設(shè)![]() ,每批游客從各自報(bào)名點(diǎn)到P島所需的運(yùn)輸總成本為T元.
,每批游客從各自報(bào)名點(diǎn)到P島所需的運(yùn)輸總成本為T元.
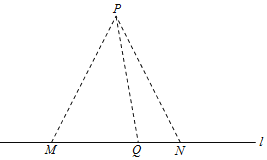
![]() 寫(xiě)出T關(guān)于
寫(xiě)出T關(guān)于![]() 的函數(shù)表達(dá)式,并指出
的函數(shù)表達(dá)式,并指出![]() 的取值范圍;
的取值范圍;
![]() 問(wèn):中轉(zhuǎn)點(diǎn)Q距離M處多遠(yuǎn)時(shí),T最小?
問(wèn):中轉(zhuǎn)點(diǎn)Q距離M處多遠(yuǎn)時(shí),T最小?
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】某生產(chǎn)企業(yè)研發(fā)了一種新產(chǎn)品,該新產(chǎn)品在某網(wǎng)店試銷一個(gè)階段后得到銷售單價(jià)![]() 和月銷售量
和月銷售量![]() 之間的一組數(shù)據(jù),如下表所示:
之間的一組數(shù)據(jù),如下表所示:
銷售單價(jià) | 9 | 9.5 | 10 | 10.5 | 11 |
月銷售量 | 11 | 10 | 8 | 6 | 5 |
(1)根據(jù)統(tǒng)計(jì)數(shù)據(jù),求出![]() 關(guān)于
關(guān)于![]() 的回歸直線方程,并預(yù)測(cè)月銷售量不低于12萬(wàn)件時(shí)銷售單價(jià)的最大值;
的回歸直線方程,并預(yù)測(cè)月銷售量不低于12萬(wàn)件時(shí)銷售單價(jià)的最大值;
(2)生產(chǎn)企業(yè)與網(wǎng)店約定:若該新產(chǎn)品的月銷售量不低于10萬(wàn)件,則生產(chǎn)企業(yè)獎(jiǎng)勵(lì)網(wǎng)店1萬(wàn)元;若月銷售量不低于8萬(wàn)件且不足10萬(wàn)件,則生產(chǎn)企業(yè)獎(jiǎng)勵(lì)網(wǎng)店5000元;若月銷售量低于8萬(wàn)件,則沒(méi)有獎(jiǎng)勵(lì).現(xiàn)用樣本估計(jì)總體,從上述5個(gè)銷售單價(jià)中任選2個(gè)銷售單價(jià),下個(gè)月分別在兩個(gè)不同的網(wǎng)店進(jìn)行銷售,求這兩個(gè)網(wǎng)店下個(gè)月獲得獎(jiǎng)勵(lì)的總額![]() 的分布列及其數(shù)學(xué)期望.
的分布列及其數(shù)學(xué)期望.
參考公式:對(duì)于一組數(shù)據(jù)![]() ,
,![]() ,…,
,…,![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘估計(jì)分別為
的斜率和截距的最小二乘估計(jì)分別為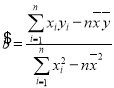 ,
,![]() .
.
參考數(shù)據(jù):![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
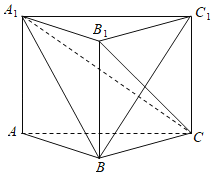
【題目】如圖,在三棱柱![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,
,![]() .
.
(Ⅰ)求證:![]() 平面
平面![]() ;
;
(Ⅱ)求異面直線![]() 與
與![]() 所成角的大小;
所成角的大小;
(Ⅲ)點(diǎn)![]() 在線段
在線段![]() 上,且
上,且![]() ,點(diǎn)
,點(diǎn)![]() 在線段
在線段![]() 上,若
上,若![]() 平面
平面![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】企業(yè)需為員工繳納社會(huì)保險(xiǎn),繳費(fèi)標(biāo)準(zhǔn)是根據(jù)職工本人上一年度月平均工資(單位:元)的![]() 繳納,
繳納,
年份 | 2014 | 2015 | 2016 | 2017 | 2018 |
t | 1 | 2 | 3 | 4 | 5 |
y | 270 | 330 | 390 | 460 | 550 |
某企業(yè)員工甲在2014年至2018年各年中每月所撒納的養(yǎng)老保險(xiǎn)數(shù)額y(單位:元)與年份序號(hào)t的統(tǒng)計(jì)如下表:
(1)求出t關(guān)于t的線性回歸方程![]() ;
;
(2)試預(yù)測(cè)2019年該員工的月平均工資為多少元?
附:回歸直線的斜率和截距的最小二乘法估計(jì)公式分別為:
(注: ,
,![]() ,其中
,其中![]() )
)
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】正四面體是側(cè)棱與底面邊長(zhǎng)都相等的正三棱錐,它的對(duì)棱互相垂直.有一個(gè)如圖所示的正四面體![]() ,E,F,G分別是棱AB,BC,CD的中點(diǎn).
,E,F,G分別是棱AB,BC,CD的中點(diǎn).

(1)求證:![]() 面EFG;
面EFG;
(2)求異面直線EG與AC所成角的大小.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)![]() ,
,![]() .
.
(1)求函數(shù)![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(2)若關(guān)于![]() 的方程
的方程![]() 有實(shí)數(shù)根,求實(shí)數(shù)
有實(shí)數(shù)根,求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com