
【題目】已知函數![]() ,
,![]() ,
,![]() 是實數.
是實數.
(Ⅰ)若![]() 在
在![]() 處取得極值,求
處取得極值,求![]() 的值;
的值;
(Ⅱ)若![]() 在區間
在區間![]() 為增函數,求
為增函數,求![]() 的取值范圍;
的取值范圍;
(Ⅲ)在(Ⅱ)的條件下,函數![]() 有三個零點,求
有三個零點,求![]() 的取值范圍.
的取值范圍.
 口算能手系列答案
口算能手系列答案科目:高中數學 來源: 題型:
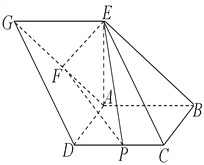
【題目】如圖,已知四邊形![]() 和
和![]() 均為平行四邊形,點
均為平行四邊形,點![]() 在平面
在平面![]() 內的射影恰好為點
內的射影恰好為點![]() ,以
,以![]() 為直徑的圓經過點
為直徑的圓經過點![]() ,
,![]() ,
,![]() 的中點為
的中點為![]() ,
,![]() 的中點為
的中點為![]() ,且
,且![]() .
.
(Ⅰ)求證:平面![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
已知曲線![]() 在平面直角坐標系
在平面直角坐標系![]() 下的參數方程為
下的參數方程為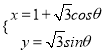 (
(![]() 為參數),以坐標原點
為參數),以坐標原點![]() 為極點,以
為極點,以![]() 軸正半軸為極軸,建立極坐標系.
軸正半軸為極軸,建立極坐標系.
(1)求曲線![]() 的普通方程及極坐標方程;
的普通方程及極坐標方程;
(2)直線![]() 的極坐標方程是
的極坐標方程是![]() ,射線
,射線![]() :
: ![]() 與曲線
與曲線![]() 交于點
交于點![]() 與直線
與直線![]() 交于點
交于點![]() ,求線段
,求線段![]() 的長.
的長.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,拋物線![]() 的焦點為
的焦點為![]() ,拋物線上一定點
,拋物線上一定點![]() .
.
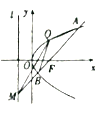
(1)求拋物線![]() 的方程及準線
的方程及準線![]() 的方程;
的方程;
(2)過焦點![]() 的直線(不經過
的直線(不經過![]() 點)與拋物線交于
點)與拋物線交于![]() 兩點,與準線
兩點,與準線![]() 交于點
交于點![]() ,記
,記![]() 的斜率分別為
的斜率分別為![]() ,問是否存在常數
,問是否存在常數![]() ,使得
,使得![]() 成立?若存在
成立?若存在![]() ,求出
,求出![]() 的值;若不存在,說明理由.
的值;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,直線
,直線![]() 經過橢圓
經過橢圓![]() 的左頂點
的左頂點![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)設直線![]() (
(![]() )交橢圓
)交橢圓![]() 于
于![]() 兩點(
兩點(![]() 不同于點
不同于點![]() ).過原點
).過原點![]() 的一條直線與直線
的一條直線與直線![]() 交于點
交于點![]() ,與直線
,與直線![]() 分別交于點
分別交于點![]() .
.
(ⅰ)當![]() 時,求
時,求![]() 的最大值;
的最大值;
(ⅱ)若![]() ,求證:點
,求證:點![]() 在一條定直線上.
在一條定直線上.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】二手經銷商小王對其所經營的![]() 型號二手汽車的使用年數
型號二手汽車的使用年數![]() 與銷售價格
與銷售價格![]() (單位:萬元/輛)進行整理,得到如下數據:
(單位:萬元/輛)進行整理,得到如下數據:

下面是![]() 關于
關于![]() 的折線圖:
的折線圖:
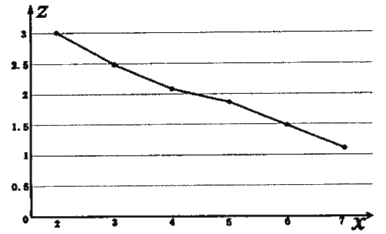
(1)由折線圖可以看出,可以用線性回歸模型擬合![]() 與
與![]() 的關系,請用相關系數加以說明;
的關系,請用相關系數加以說明;
(2)求![]() 關于
關于![]() 的回歸方程并預測某輛
的回歸方程并預測某輛![]() 型號二手汽車當使用年數為9年時售價大約為多少?(
型號二手汽車當使用年數為9年時售價大約為多少?(![]() 、
、![]() 小數點后保留兩位有效數字).
小數點后保留兩位有效數字).
(3)基于成本的考慮,該型號二手車的售價不得低于7118元,請根據(2)求出的回歸方程預測在收購該型號二手車時車輛的使用年數不得超過多少年?
參考公式:回歸方程![]() 中斜率和截距的最小二乘估計公式分別為:
中斜率和截距的最小二乘估計公式分別為:
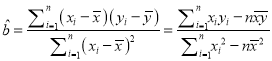 ,
,![]() .
. 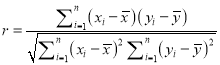 .
.
參考數據:
![]() ,
,![]() ,
,![]() ,
,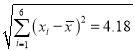 ,
,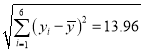 ,
,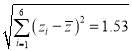 ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線![]() ,直線
,直線![]() 交
交![]() 于
于![]() 兩點,
兩點, ![]() 是
是![]() 的中點,過
的中點,過![]() 作
作![]() 軸的垂線交
軸的垂線交![]() 于
于![]() 點.
點.

(1)證明:拋物線![]() 在
在![]() 點處的切線與
點處的切線與![]() 平行;
平行;
(2)是否存在實數![]() ,使以
,使以![]() 為直徑的圓
為直徑的圓![]() 經過
經過![]() 點?若存在,求出
點?若存在,求出![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com