
【題目】如圖,拋物線![]() 的焦點為
的焦點為![]() ,拋物線上一定點
,拋物線上一定點![]() .
.
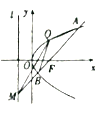
(1)求拋物線![]() 的方程及準線
的方程及準線![]() 的方程;
的方程;
(2)過焦點![]() 的直線(不經過
的直線(不經過![]() 點)與拋物線交于
點)與拋物線交于![]() 兩點,與準線
兩點,與準線![]() 交于點
交于點![]() ,記
,記![]() 的斜率分別為
的斜率分別為![]() ,問是否存在常數
,問是否存在常數![]() ,使得
,使得![]() 成立?若存在
成立?若存在![]() ,求出
,求出![]() 的值;若不存在,說明理由.
的值;若不存在,說明理由.
 學而優銜接教材南京大學出版社系列答案
學而優銜接教材南京大學出版社系列答案 小學課堂作業系列答案
小學課堂作業系列答案 金博士一點全通系列答案
金博士一點全通系列答案科目:高中數學 來源: 題型:
【題目】類比平面內正三角形的“三邊相等,三內角相等”的性質,可推出正四面體的下列一些性質,你認為比較恰當的是( )
①各棱長相等,同一頂點上的任兩條棱的夾角都相等;②各個面都是全等的正三角形,相鄰兩個面所成的二面角都相等;③各個面都是全等的正三角形,同一頂點上的任兩條棱的夾角都相等。
A. ① B. ②③ C. ①② D. ①②③
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,其中
,其中![]()
(1)當![]() 時,求函數
時,求函數![]() 在
在![]() 處的切線方程;
處的切線方程;
(2)若函數![]() 在定義域上有且只有一個極值點,求實數
在定義域上有且只有一個極值點,求實數![]() 的取值范圍;
的取值范圍;
(3)若對任意![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的兩個焦點分別為
的兩個焦點分別為![]() ,離心率為
,離心率為![]() .設過點
.設過點![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 相交于不同兩點
相交于不同兩點![]() ,
, ![]() 周長為
周長為![]() .
.
(Ⅰ)求橢圓C的標準方程;
(Ⅱ)已知點![]() ,證明:當直線
,證明:當直線![]() 變化時,總有TA與
變化時,總有TA與![]() 的斜率之和為定值.
的斜率之和為定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】宿州市教體局為了了解![]() 屆高三畢業生學生情況,利用分層抽樣抽取
屆高三畢業生學生情況,利用分層抽樣抽取![]() 位學生數學學業水平測試成績作調查,制作了成績頻率分布直方圖,如圖所示,其中成績分組區間是:
位學生數學學業水平測試成績作調查,制作了成績頻率分布直方圖,如圖所示,其中成績分組區間是:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.

(Ⅰ)求圖中![]() 的值;
的值;
(Ⅱ)根據直方圖估計宿州市![]() 屆高三畢業生數學學業水平測試成績的平均分;
屆高三畢業生數學學業水平測試成績的平均分;
(Ⅲ)在抽取的![]() 人中,從成績在
人中,從成績在![]() 和
和![]() 的學生中隨機選取
的學生中隨機選取![]() 人,求這
人,求這![]() 人成績差別不超過
人成績差別不超過![]() 分的概率.
分的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
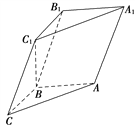
【題目】如圖,在三棱柱ABCA1B1C1中,已知AB⊥側面BB1C1C,AB=BC=1,BB1=2,∠BCC1=![]() .
.
(1)求證:C1B⊥平面ABC;
設![]() (0≤λ≤1),且平面AB1E與BB1E所成的銳二面角的大小為30°,
(0≤λ≤1),且平面AB1E與BB1E所成的銳二面角的大小為30°,
試求λ的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
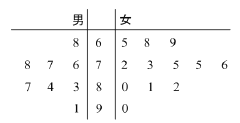
【題目】某學校舉行物理競賽,有8名男生和12名女生報名參加,將這20名學生的成績制成莖葉圖如圖所示.成績不低于80分的學生獲得“優秀獎”,其余獲“紀念獎”.
(Ⅰ)求出8名男生的平均成績和12 名女生成績的中位數;
(Ⅱ)按照獲獎類型,用分層抽樣的方法從這20名學生中抽取5人,再從選出的5人中任選3人,求恰有1人獲“優秀獎”的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲參加A,B,C三個科目的學業水平考試,其考試成績合格的概率如下表,假設三個科目的考試甲是否成績合格相互獨立.
科目A | 科目B | 科目C | |
甲 |
|
|
|
(I)求甲至少有一個科目考試成績合格的概率;
(Ⅱ)設甲參加考試成績合格的科目數量為X,求X的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】【2014課標全國Ⅰ,文12】已知函數f(x)=ax3-3x2+1,若f(x)存在唯一的零點x0,且x0>0,則a的取值范圍是( ).
A.(2,+∞) B.(1,+∞)
C.(-∞,-2) D.(-∞,-1)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com