
【題目】下列四個命題:(1)函數f(x)在[0,+∞)上是增函數,在(﹣∞,0)上也是增函數,所以f(x)在R上是增函數;(2)若函數f(x)=ax2+bx+2與x軸沒有交點,則b2﹣8a<0,且a>0; (3)y=x2﹣2|x|﹣3的遞增區間為[1,+∞);(4)函數y=lg10x和函數y=elnx表示相同函數.其中正確命題的個數是( )
A.3
B.2
C.1
D.0
【答案】D
【解析】解:對于(1),如函數f(x)=﹣ ![]() 在[0,+∞)上是增函數,在(﹣∞,0)上也是增函數,但不能說f(x)在R上是增函數,故錯;對于(2),若函數f(x)=ax2+bx+2與x軸沒有交點,則b2﹣8a<0,a>0或a<0都可以,還有a=b=0時也滿足,故錯;
在[0,+∞)上是增函數,在(﹣∞,0)上也是增函數,但不能說f(x)在R上是增函數,故錯;對于(2),若函數f(x)=ax2+bx+2與x軸沒有交點,則b2﹣8a<0,a>0或a<0都可以,還有a=b=0時也滿足,故錯;
對于 (3),∵y=x2﹣2|x|﹣3是偶函數其遞增區間為[1,+∞),(﹣∞,﹣1],故錯;
對于(4),函數y=lg10x (x∈R),函數y=elnx(x>0),定義與不同,故錯.
故選:D.
【考點精析】認真審題,首先需要了解命題的真假判斷與應用(兩個命題互為逆否命題,它們有相同的真假性;兩個命題為互逆命題或互否命題,它們的真假性沒有關系).


科目:高中數學 來源: 題型:
【題目】在直角坐標系中,以坐標原點O為極點,x軸的非負半軸為極軸建立極坐標系,直線l的極坐標方程為ρsin(θ+![]() )=
)=![]() ,曲線C的參數方程為
,曲線C的參數方程為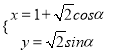 (α為參數).
(α為參數).
(1)求直線l的普通方程;
(2)若P是曲線C上的動點,求點P到直線l的最大距離及點P的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在探究實系數一元二次方程的根與系數的關系時,可按下述方法進行:
設實系數一元二次方程![]() ……①
……①
在復數集![]() 內的根為
內的根為![]() ,
, ![]() ,則方程①可變形為
,則方程①可變形為![]() ,
,
展開得![]() .……②
.……②
比較①②可以得到: 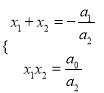
類比上述方法,設實系數一元![]() 次方程
次方程![]() (
(![]() 且
且![]() )在復數集
)在復數集![]() 內的根為
內的根為![]() ,
, ![]() ,…,
,…, ![]() ,則這
,則這![]() 個根的積
個根的積![]() __________.
__________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一企業從某條生產線上隨機抽取30件產品,測量這些產品的某項技術指標值![]() ,得到如下的頻數分布表:
,得到如下的頻數分布表:
|
|
|
|
|
頻數 | 2 | 6 | 18 | 4 |
(I)估計該技術指標值的平均數和眾數(以各組區間的中點值代表該組的取值);
(II) 若![]() 或
或![]() ,則該產品不合格,其余的是合格產品,從不合格的產品中隨機抽取2件,求抽取的2件產品中技術指標值小于
,則該產品不合格,其余的是合格產品,從不合格的產品中隨機抽取2件,求抽取的2件產品中技術指標值小于![]() 的產品恰有1件的概率.
的產品恰有1件的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某同學在研究函數f(x)= ![]() ﹣1(x∈R)時,得出了下面4個結論:①等式f(﹣x)=f(x)在x∈R時恒成立;②函數f(x)在x∈R上的值域為(﹣1,1];③曲線y=f(x)與g(x)=2x﹣2僅有一個公共點;④若f(x)=
﹣1(x∈R)時,得出了下面4個結論:①等式f(﹣x)=f(x)在x∈R時恒成立;②函數f(x)在x∈R上的值域為(﹣1,1];③曲線y=f(x)與g(x)=2x﹣2僅有一個公共點;④若f(x)= ![]() ﹣1在區間[a,b](a,b為整數)上的值域是[0,1],則滿足條件的整數數對(a,b)共有5對.其中正確結論的序號有(請將你認為正確的結論的序號都填上).
﹣1在區間[a,b](a,b為整數)上的值域是[0,1],則滿足條件的整數數對(a,b)共有5對.其中正確結論的序號有(請將你認為正確的結論的序號都填上).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】己知函數f(x)=loga(3x+1),g(x)=loga(1﹣3x),(a>0且a≠1).
(1)求函數F(x)=f(x)﹣g(x)的定義域;
(2)判斷F(x)=f(x)﹣g(x)的奇偶性,并說明理由4;
(3)確定x為何值時,有f(x)﹣g(x)>0.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】提高過江大橋的車輛通行能力可改善整個城市的交通狀況,在一般情況下,大橋上的車流速度v(單位:千米/小時)是車流密度x(單位:輛/千米)的函數,當橋上的車流密度達到200輛/千米時,造成堵塞,此時車流速度為0;當車流密度不超過20輛/千米時,車流速度為60千米/小時,研究表明:當20≤x≤200時,車流速度v是車流密度x的一次函數.
(Ⅰ)當0≤x≤200時,求函數v(x)的表達式;
(Ⅱ)當車流密度x為多大時,車流量(單位時間內通過橋上某觀測點的車輛數,單位:輛/小時)f(x)=xv(x)可以達到最大,并求出最大值.(精確到1輛/小時).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com