
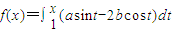 在
在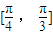 上為增函數的概率是( )
上為增函數的概率是( )


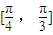 上為增函數,導數在區間
上為增函數,導數在區間 上大于等于0恒成立.求出滿足a,b的關系式,最后把a看成橫軸,b看成縱軸,a,b在一象限圍成邊長為2的正方形的面積為總的基本事件,a,b關系式與正方形圍成的面積為滿足條件的基本事件,用面積之比求出概率.
上大于等于0恒成立.求出滿足a,b的關系式,最后把a看成橫軸,b看成縱軸,a,b在一象限圍成邊長為2的正方形的面積為總的基本事件,a,b關系式與正方形圍成的面積為滿足條件的基本事件,用面積之比求出概率.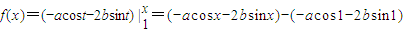 ,
,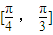 上恒成立,則函數f(x)在區間
上恒成立,則函數f(x)在區間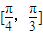 是增函數.
是增函數.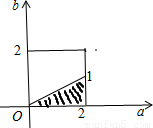
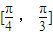 上均大于0,
上均大于0,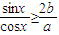 ,即
,即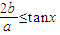 .
.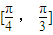 上恒成立?
上恒成立? ,
,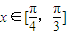 .
.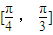 上的最小值為
上的最小值為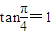 ,∴
,∴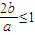 ,
,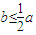 .
.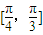 上為增函數的概率為
上為增函數的概率為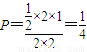 .
.

湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com