
【題目】(12分)
已知函數![]() (a為實數).
(a為實數).
(1)當![]() 時,求函數
時,求函數![]() 的圖像在
的圖像在![]() 處的切線方程;
處的切線方程;
(2)求![]() 在區間
在區間![]() 上的最小值;
上的最小值;
(3)若存在兩個不等實數![]() ,使方程
,使方程![]() 成立,求實數a的取值范圍.
成立,求實數a的取值范圍.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】從標準質量為500g的一批洗衣粉中,隨機抽查了50袋,測得的質量數據如下(單位:g):
494 498 493 494 496 492 490 490 500 499 494 495 482 485 502
493 505 485 501 491 493 500 509 512 484 509 510 494 497 498
504 498 483 510 503 497 502 498 497 500 493 499 505 493 491
497 515 503 498 518
(1)找出這組數的最值,求出極差;
(2)以![]() 為第一個分組的區間,作出這組數的頻率分布表.
為第一個分組的區間,作出這組數的頻率分布表.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某人經營一個抽獎游戲,顧客花費3元錢可購買一次游戲機會,每次游戲中,顧客從標有黑1、黑2、黑3、黑4、紅1、紅3的6張卡片中隨機抽取2張,并根據摸出的卡片的情況進行兌獎,經營者將顧客抽到的卡片情況分成以下類別:![]() :同花順,即卡片顏色相同且號碼相鄰;
:同花順,即卡片顏色相同且號碼相鄰;![]() :同花,即卡片顏色相同,但號碼不相鄰;
:同花,即卡片顏色相同,但號碼不相鄰;![]() :順子,即卡片號碼相鄰,但顏色不同;
:順子,即卡片號碼相鄰,但顏色不同;![]() :對子,即兩張卡片號碼相同;
:對子,即兩張卡片號碼相同;![]() :其它,即
:其它,即![]() ,
,![]() ,
,![]() ,
,![]() 以外的所有可能情況,若經營者打算將以上五種類別中最不容易發生的一種類別對應顧客中一等獎,最容易發生的一種類別對應顧客中二等獎,其他類別對應顧客中三等獎.
以外的所有可能情況,若經營者打算將以上五種類別中最不容易發生的一種類別對應顧客中一等獎,最容易發生的一種類別對應顧客中二等獎,其他類別對應顧客中三等獎.
(1)一、二等獎分別對應哪一種類別?(寫出字母即可)
(2)若經營者規定:中一、二、三等獎,分別可獲得價值9元、3元、1元的獎品,假設某天參與游戲的顧客為300人次,試估計經營者這一天的盈利.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓C:![]() +
+![]() =1(a>b>0)的離心率為
=1(a>b>0)的離心率為![]() ,且短軸長為6.
,且短軸長為6.
(1)求橢圓的標準方程;
(2)是否存在斜率為1的直線l,使得l與曲線C相交于A,B兩點,且以AB為直徑的圓恰好經過原點?若存在,求出直線l的方程;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(12分)
已知拋物線![]() 的焦點F與橢圓
的焦點F與橢圓![]() 的一個焦點重合,點
的一個焦點重合,點![]() 在拋物線上,過焦點F的直線l交拋物線于A,B兩點.
在拋物線上,過焦點F的直線l交拋物線于A,B兩點.
(1)求拋物線C的標準方程以及![]() 的值.
的值.
(2)記拋物線的準線![]() 軸交于點H,試問是否存在常數
軸交于點H,試問是否存在常數![]() ,使得
,使得![]() ,且
,且![]() 都成立.若存在,求出
都成立.若存在,求出![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓![]() 的方程為
的方程為![]() ,點
,點![]() ,點M為圓
,點M為圓![]() 上的任意一點,線段
上的任意一點,線段![]() 的垂直平分線與線段
的垂直平分線與線段![]() 相交于點N.
相交于點N.
(1)求點N的軌跡C的方程.
(2)已知點![]() ,過點A且斜率為k的直線
,過點A且斜率為k的直線![]() 交軌跡C于
交軌跡C于![]() 兩點,以
兩點,以![]() 為鄰邊作平行四邊形
為鄰邊作平行四邊形![]() ,是否存在常數k,使得點B在軌跡C上,若存在,求k的值;若不存在,說明理由.
,是否存在常數k,使得點B在軌跡C上,若存在,求k的值;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某地區發現某污染源,相關部門對污染情況進行調查研究后,發現一天中污染指數![]() 與時刻x(時)的函數關系為
與時刻x(時)的函數關系為![]() ,其中a是與氣象有關的參數,且
,其中a是與氣象有關的參數,且![]() .按規定,若每天污染指數不超過2,則環保合格,否則需要整改.如果以每天中
.按規定,若每天污染指數不超過2,則環保合格,否則需要整改.如果以每天中![]() 的最大值作為當天的污染指數,并記為
的最大值作為當天的污染指數,并記為![]() ,那么該地區污染指數的超標情況為________.
,那么該地區污染指數的超標情況為________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓具有以下性質:設A,B是圓C:![]() 上關于原點對稱的兩點,點P是圓上的任意一點.若直線PA,PB的斜率都存在并分別記為
上關于原點對稱的兩點,點P是圓上的任意一點.若直線PA,PB的斜率都存在并分別記為![]() ,
,![]() ,則
,則![]() =﹣1,是與點P的位置無關的定值.
=﹣1,是與點P的位置無關的定值.
(1)試類比圓的上述性質,寫出橢圓![]() 的一個類似性質,并加以證明;
的一個類似性質,并加以證明;
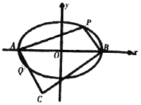
(2)如圖,若橢圓M的標準方程為![]() ,點P在橢圓M上且位于第一象限,點A,B分別為橢圓長軸的兩個端點,過點A,B分別作
,點P在橢圓M上且位于第一象限,點A,B分別為橢圓長軸的兩個端點,過點A,B分別作![]() ⊥PA,
⊥PA,![]() ⊥PB,直線
⊥PB,直線![]() ,
,![]() 交于點C,直線
交于點C,直線![]() 與橢圓M的另一交點為Q,且
與橢圓M的另一交點為Q,且![]() ,求
,求![]() 的取值范圍(可直接使用(1)中證明的結論).
的取值范圍(可直接使用(1)中證明的結論).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某醫藥開發公司實驗室有![]() 瓶溶液,其中
瓶溶液,其中![]() 瓶中有細菌
瓶中有細菌![]() ,現需要把含有細菌
,現需要把含有細菌![]() 的溶液檢驗出來,有如下兩種方案:
的溶液檢驗出來,有如下兩種方案:
方案一:逐瓶檢驗,則需檢驗![]() 次;
次;
方案二:混合檢驗,將![]() 瓶溶液分別取樣,混合在一起檢驗,若檢驗結果不含有細菌
瓶溶液分別取樣,混合在一起檢驗,若檢驗結果不含有細菌![]() ,則
,則![]() 瓶溶液全部不含有細菌
瓶溶液全部不含有細菌![]() ;若檢驗結果含有細菌
;若檢驗結果含有細菌![]() ,就要對這
,就要對這![]() 瓶溶液再逐瓶檢驗,此時檢驗次數總共為
瓶溶液再逐瓶檢驗,此時檢驗次數總共為![]() .
.
(1)假設![]() ,采用方案一,求恰好檢驗3次就能確定哪兩瓶溶液含有細菌
,采用方案一,求恰好檢驗3次就能確定哪兩瓶溶液含有細菌![]() 的概率;
的概率;
(2)現對![]() 瓶溶液進行檢驗,已知每瓶溶液含有細菌
瓶溶液進行檢驗,已知每瓶溶液含有細菌![]() 的概率均為
的概率均為![]() .
.
若采用方案一.需檢驗的總次數為![]() ,若采用方案二.需檢驗的總次數為
,若采用方案二.需檢驗的總次數為![]() .
.
(i)若![]() 與
與![]() 的期望相等.試求
的期望相等.試求![]() 關于
關于![]() 的函數解析式
的函數解析式![]() ;
;
(ii)若![]() ,且采用方案二總次數的期望小于采用方案一總次數的期望.求
,且采用方案二總次數的期望小于采用方案一總次數的期望.求![]() 的最大值.
的最大值.
參考數據:![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com