
【題目】設函數![]() ,
, ![]() =
= ![]() .
.
(Ⅰ)求函數![]() 的單調區間;
的單調區間;
(Ⅱ)若函數![]() 有兩個零點
有兩個零點![]() .
.
(1)求滿足條件的最小正整數![]() 的值;
的值;
(2)求證: ![]() .
.
【答案】(Ⅰ)![]() 的單調增區間為
的單調增區間為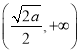 ,單調減區間為
,單調減區間為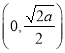 ;
;
(Ⅱ)(1)3;(2)見解析.
【解析】試題分析:
(Ⅰ)求單調區間,只要求得導數![]() ,通過討論
,通過討論![]() 的范圍(
的范圍(![]() 和
和![]() )可解不等式
)可解不等式![]() 和不等式
和不等式![]() ,從而得單調區間;
,從而得單調區間;
(Ⅱ)(1)求得![]() ,由
,由![]() 有兩個零點得
有兩個零點得![]() ,
, ![]() 的最小值為
的最小值為![]() ,且
,且![]() , 由此可得
, 由此可得![]() ,由函數
,由函數![]() 是增函數,通過估值可得最小正整數
是增函數,通過估值可得最小正整數![]() 的值;(2)證明
的值;(2)證明![]() ,設
,設![]() ,由
,由![]() ,可把
,可把![]() 用
用![]() 表示,不等式
表示,不等式![]() 中的
中的![]() 可替換,然后變形為
可替換,然后變形為![]() 的不等式,設
的不等式,設![]() ,則
,則![]() ,只要證相應地關于
,只要證相應地關于![]() 的不等式在
的不等式在![]() 上成立,這又可用導數研究相應的函數得出.
上成立,這又可用導數研究相應的函數得出.
試題解析:
(Ⅰ)![]() .
.
當![]() 時,
時, ![]() 在
在![]() 上恒成立,所以函數
上恒成立,所以函數![]() 單調遞增區間為
單調遞增區間為![]() ,
,
此時![]() 無單調減區間.
無單調減區間.
當![]() 時,由
時,由![]() ,得
,得![]() ,
, ![]() ,得
,得![]() ,
,
所以函數![]() 的單調增區間為
的單調增區間為 ,單調減區間為
,單調減區間為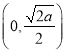 .
.
(Ⅱ)(1)![]() .
.
因為函數![]() 有兩個零點,所以
有兩個零點,所以![]() ,此時函數
,此時函數![]() 在
在![]() 單調遞增, 在
單調遞增, 在![]() 單調遞減.
單調遞減.
所以![]() 的最小值
的最小值![]() ,即
,即![]() .
.
因為![]() ,所以
,所以![]() .
.
令![]() ,顯然
,顯然![]() 在
在![]() 上為增函數,且
上為增函數,且
![]() ,所以存在
,所以存在![]() .
.
當![]() 時,
時, ![]() ;當
;當![]() 時,
時, ![]() ,所以滿足條件的最小正整數
,所以滿足條件的最小正整數![]() .
.
又當![]() 時,
時, ![]() ,所以
,所以![]() 時,
時, ![]() 有兩個零點.
有兩個零點.
綜上所述,滿足條件的最小正整數![]() 的值為3.
的值為3.
(2)證明 :不妨設![]() ,于是
,于是![]()
即![]() ,
,
![]() .
.
所以![]() .
.
因為![]() ,當
,當![]() 時,
時, ![]() ,當
,當![]() 時,
時, ![]() ,
,
故只要證![]() >
>![]() 即可,即證明
即可,即證明![]() ,
,
即證![]() ,
,
也就是證![]() .
.
設![]() .
.
令![]() ,則
,則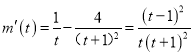 .
.
因為![]() ,所以
,所以![]() ,
,
當且僅當![]() 時,
時, ![]() ,
,
所以![]() 在
在![]() 上是增函數.
上是增函數.
又![]() ,所以當
,所以當![]() 總成立,所以原題得證.
總成立,所以原題得證.


 應用題天天練四川大學出版社系列答案
應用題天天練四川大學出版社系列答案科目:高中數學 來源: 題型:
【題目】已知函數f(x)=ax2+1(a>0),g(x)=x3+bx.
(1)若曲線y=f(x)與曲線y=g(x)在它們的交點(1,c)處具有公共切線,求a,b的值;
(2)當a=3,b=-9時,若函數f(x)+g(x)在區間[k,2]上的最大值為28,求k的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,
, ![]() .
.
(Ⅰ)當![]() 時,求
時,求![]() 在
在![]() 處的切線方程;
處的切線方程;
(Ⅱ)若![]() 且函數
且函數![]() 有且僅有一個零點,求實數
有且僅有一個零點,求實數![]() 的值;
的值;
(Ⅲ)在(Ⅱ)的條件下,若![]() 時,
時, ![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖1,在正方形![]() 中,點
中,點![]() 分別是
分別是![]() 的中點,
的中點,![]() 與
與![]() 交于點
交于點![]() ,點
,點![]() 分別在線段
分別在線段![]() 上,且
上,且![]() .將
.將![]() 分別沿
分別沿![]() 折起,使點
折起,使點![]() 重合于點
重合于點![]() ,如圖2所示.
,如圖2所示.
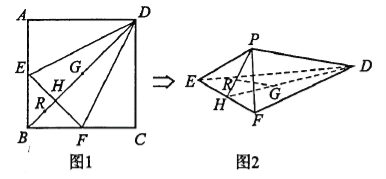
(1)求證:![]() 平面
平面![]() ;
;
(2)若正方形![]() 的邊長為4,求三棱錐
的邊長為4,求三棱錐![]() 的內切球的半徑.
的內切球的半徑.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】中石化集團獲得了某地深海油田塊的開采權,集團在該地區隨機初步勘探了部分幾口井,取得了地質資料,進入全面勘探時期后,集團按網絡點米布置井位進行全面勘探,由于勘探一口井的費用很高,如果新設計的井位與原有井位重合或接近,便利用舊井的地質資料,不必打這口斷井,以節約勘探費用,勘探初期數據資料見下表:
井號 |
|
|
|
|
|
|
坐標 |
|
|
|
|
|
|
鉆探深度 |
|
|
|
|
|
|
出油量 |
|
|
|
|
|
|
(1)![]() ~
~![]() 號舊井位置線性分布,借助前5組數據求得回歸直線方程為
號舊井位置線性分布,借助前5組數據求得回歸直線方程為![]() ,求
,求![]() ,并估計
,并估計![]() 的預報值;
的預報值;
(2)現準備勘探新井![]() ,若通過
,若通過![]() 號并計算出的
號并計算出的![]() 的值(
的值(![]() 精確到
精確到![]() )與(1)中
)與(1)中![]() 的值差不超過
的值差不超過![]() ,則使用位置最接近的已有舊井
,則使用位置最接近的已有舊井![]() ,否則在新位置打開,請判斷可否使用舊井?
,否則在新位置打開,請判斷可否使用舊井?
(參考公式和計算結果: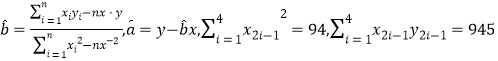 )
)
(3)設出油量與勘探深度的比值![]() 不低于20的勘探井稱為優質井,那么在原有
不低于20的勘探井稱為優質井,那么在原有![]() 口井中任意勘探
口井中任意勘探![]() 口井,求勘探優質井數
口井,求勘探優質井數![]() 的分布列與數學期望.
的分布列與數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】上世紀八十年代初, 鄧小平同志曾指出“在人才的問題上,要特別強調一下,必須打破常規去發現、選拔和培養杰出的人才”. 據此,經省教育廳批準,某中學領導審時度勢,果斷作出于1985年開始施行超常實驗班教學試驗的決定.一時間,學生興奮,教師欣喜,家長歡呼,社會熱議.該中學實驗班一路走來,可謂風光無限,碩果累累,尤其值得一提的是,1990年,全國共招收150名少年大學生,該中學就有19名實驗班學生被錄取,占全國的十分之一,轟動海內外.設該中學超常實驗班學生第x年被錄取少年大學生的人數為y.
左下表為該中學連續5年實驗班學生被錄取少年大學生人數,求y關于x的線性回歸方程,并估計第6年該中學超常實驗班學生被錄取少年大學生人數;
年份序號x | 1 | 2 | 3 | 4 | 5 |
錄取人數y | 10 | 11 | 14 | 16 | 19 |
附1: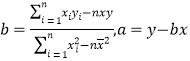
![]()
下表是從該校已經畢業的100名高中生錄取少年大學生人數與是否接受超常實驗班教育得到
2×2列聯表,完成上表,并回答:是否有95%以上的把握認為“錄取少年大學生人數與是否接受超常實驗班教育有關系”.
附2:
接受超常實驗班教育 | 未接受超常實驗班教育 | 合計 | |
錄取少年大學生 | 60 | 80 | |
未錄取少年大學生 | 10 | ||
合計 | 30 | 100 |
![]()
| 0.50 | 0.40 | 0.10 | 005 |
| 0.455 | 0.708 | 2.706 | 3.841 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若方程![]() 所表示的曲線為C,給出下列四個命題:
所表示的曲線為C,給出下列四個命題:
①若C為橢圓,則1<t<4且t≠![]() ;
;
②若C為雙曲線,則t>4或t<1;
③曲線C不可能是圓;
④若C表示橢圓,且長軸在x軸上,則1<t<![]() .
.
其中正確的命題是________(把所有正確命題的序號都填在橫線上).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知兩個無窮數列![]() 和
和![]() 的前
的前![]() 項和分別為
項和分別為![]() ,
,![]() ,
,![]() ,
,![]() ,對任意的
,對任意的![]() ,都有
,都有![]() .
.
(1)求數列![]() 的通項公式;
的通項公式;
(2)若![]() 為等差數列,對任意的
為等差數列,對任意的![]() ,都有
,都有![]() .證明:
.證明:![]() ;
;
(3)若![]() 為等比數列,
為等比數列,![]() ,
,![]() ,求滿足
,求滿足![]() 的
的![]() 值.
值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com