
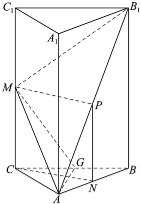
【題目】如圖,已知三棱柱ABC﹣A1B1C1中,AA1⊥平面ABC,AC=BC,M,N分別是棱CC1,AB的中點.
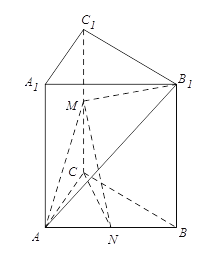
(1)求證:CN⊥平面ABB1A1;
(2)求證:CN∥平面AMB1.
【答案】(1)見解析;(2)見解析.
【解析】試題分析:(1)證明AA1⊥CN,CN⊥AB,即可證明CN⊥平面ABB1A1;
(2)設AB1的中點為P,連接NP、MP,利用三角形中位線的性質,可得線線平行,利用線面平行的判定,可得CN∥平面AMB1.
證明:(1)∵三棱柱ABC﹣A1B1C1中,AA1⊥平面ABC,CN平面ABC,
∴AA1⊥CN,
∵AC=BC,N是棱AB的中點,
∴CN⊥AB,
∵AA1∩AB=A,
∴CN⊥平面ABB1A1;
(2)設AB1的中點為P,連接NP、MP
∵M、N分別是棱CC1、AB的中點
∴CM∥![]() AA1,且CM=
AA1,且CM=![]() AA1,NP∥
AA1,NP∥![]() AA1,且NP=
AA1,且NP=![]() AA1,
AA1,
∴CM∥NP,CM=NP
∴CNPM是平行四邊形,∴CN∥MP
∵CN平面AMB1,MP平面AMB1,
∴CN∥平面AMB1.


科目:高中數學 來源: 題型:
【題目】如圖是2017年第一季度五省![]() 情況圖,則下列陳述正確的是( )
情況圖,則下列陳述正確的是( )
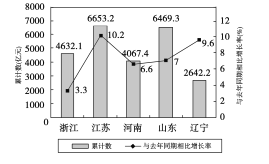
①2017年第一季度 ![]() 總量和增速均居同一位的省只有1個;
總量和增速均居同一位的省只有1個;
②與去年同期相比,2017年第一季度五個省的![]() 總量均實現了增長;
總量均實現了增長;
③去年同期的![]() 總量前三位是江蘇、山東、浙江;
總量前三位是江蘇、山東、浙江;
④2016年同期浙江的![]() 總量也是第三位.
總量也是第三位.
A. ①② B. ②③④ C. ②④ D. ①③④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
: ![]() 的上下兩個焦點分別為
的上下兩個焦點分別為![]() ,
, ![]() ,過點
,過點![]() 與
與![]() 軸垂直的直線交橢圓
軸垂直的直線交橢圓![]() 于
于![]() 、
、![]() 兩點,
兩點, ![]() 的面積為
的面積為![]() ,橢圓
,橢圓![]() 的離心力為
的離心力為![]() .
.
(Ⅰ)求橢圓![]() 的標準方程;
的標準方程;
(Ⅱ)已知![]() 為坐標原點,直線
為坐標原點,直線![]() :
: ![]() 與
與![]() 軸交于點
軸交于點![]() ,與橢圓
,與橢圓![]() 交于
交于![]() ,
, ![]() 兩個不同的點,若存在實數
兩個不同的點,若存在實數![]() ,使得
,使得![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 的一條對稱軸為
的一條對稱軸為![]() ,且最高點的縱坐標是
,且最高點的縱坐標是![]() .
.
(1)求![]() 的最小值及此時函數
的最小值及此時函數![]() 的最小正周期、初相;
的最小正周期、初相;
(2)在(1)的情況下,設![]() ,求函數
,求函數![]() 在
在![]() 上的最大值和最小值.
上的最大值和最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
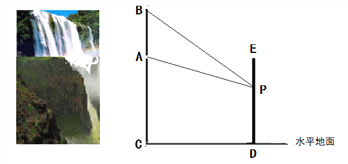
【題目】南京市江北新區計劃在一個豎直長度為20米的瀑布![]() 正前方修建一座觀光電梯
正前方修建一座觀光電梯![]() 。如圖所示,瀑布底部
。如圖所示,瀑布底部![]() 距離水平地面的高度
距離水平地面的高度![]() 為60米,電梯上設有一個安全拍照口
為60米,電梯上設有一個安全拍照口![]() ,
, ![]() 上升的最大高度為60米。設
上升的最大高度為60米。設![]() 距離水平地面的高度為
距離水平地面的高度為![]() 米,
米, ![]() 處拍照瀑布的視角
處拍照瀑布的視角![]() 為
為![]() 。攝影愛好者發現,要使照片清晰,視角
。攝影愛好者發現,要使照片清晰,視角![]() 不能小于
不能小于![]() 。
。
(1)當![]() 米時,視角
米時,視角![]() 恰好為
恰好為![]() ,求電梯和山腳的水平距離
,求電梯和山腳的水平距離![]() 。
。
(2)要使電梯拍照口![]() 的高度
的高度![]() 在52米及以上時,拍出的照片均清晰,請求出電梯和山腳的水平距離
在52米及以上時,拍出的照片均清晰,請求出電梯和山腳的水平距離![]() 的取值范圍。
的取值范圍。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校舉辦“中國詩詞大賽”活動,某班派出甲乙兩名選手同時參加比賽. 大賽設有15個詩詞填空題,其中“唐詩”、“宋詞”和“毛澤東詩詞”各5個.每位選手從三類詩詞中各任選1個進行作答,3個全答對選手得3分,答對2個選手得2分,答對1個選手得1分,一個都沒答對選手得0分. 已知“唐詩”、“宋詞”和“毛澤東詩詞”中甲能答對的題目個數依次為5,4,3,乙能答對的題目個數依此為4,5,4,假設每人各題答對與否互不影響,甲乙兩人答對與否也互不影響.
求:(1)甲乙兩人同時得到3分的概率;
(2)甲乙兩人得分之和![]() 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com