
【題目】已知數列![]() 的滿足
的滿足![]() ,前
,前![]() 項的和為
項的和為![]() ,且
,且![]() .
.
(1)求![]() 的值;
的值;
(2)設![]() ,證明:數列
,證明:數列![]() 是等差數列;
是等差數列;
(3)設![]() ,若
,若![]() ,求對所有的正整數
,求對所有的正整數![]() 都有
都有![]() 成立的
成立的![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() ;(2)見解析;(3)
;(2)見解析;(3)![]() .
.
【解析】試題分析:(1)令![]() 得
得![]() (2) 因為
(2) 因為![]() ,所以
,所以![]() ①.所以
①.所以![]() ②,由②-①,得
②,由②-①,得![]() .因為
.因為![]() ,所以
,所以![]() .所以
.所以![]() ,即
,即![]() ,
,
即![]() 即可得證(3)由(2)知,因為
即可得證(3)由(2)知,因為![]() ,所以數列
,所以數列![]() 的通項公式為
的通項公式為![]() .因為
.因為![]() ,所以
,所以![]() ,所以
,所以![]() ,所以數列
,所以數列![]() 是常數列. 由
是常數列. 由![]() ,所以
,所以![]() .所以
.所以![]() .研究數列
.研究數列![]() 的單調性求出最小值,變量分離
的單調性求出最小值,變量分離![]() 即可得解.
即可得解.
試題解析:
(1)令![]() 得
得![]() .
.
(2)因為![]() ,所以
,所以![]() ①.
①.
所以![]() ②,
②,
由②-①,得![]() .
.
因為![]() ,所以
,所以![]() .
.
所以![]() ,即
,即![]() ,
,
即![]() ,所以數列
,所以數列![]() 是公差為1的等差數列.
是公差為1的等差數列.
(3)由(2)知,因為![]() ,所以數列
,所以數列![]() 的通項公式為
的通項公式為![]() .
.
因為![]() ,所以
,所以![]() ,
,
所以![]() ,所以數列
,所以數列![]() 是常數列.
是常數列.
由![]() ,所以
,所以![]() .
.
所以![]() .
.
因為![]()
所以數列![]() 為單調遞增數列
為單調遞增數列
當![]() 時,
時, ![]() ,即
,即![]() 的最小值為
的最小值為![]()
由![]() ,所以
,所以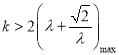 ,
,
而當![]() 時,
時, ![]() 在
在![]() 遞減,
遞減, ![]() 遞增,所以
遞增,所以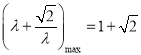 ,
,
當且僅當![]() 或
或![]() 時取得,故
時取得,故![]() .
.


 名師指導期末沖刺卷系列答案
名師指導期末沖刺卷系列答案科目:高中數學 來源: 題型:
【題目】[選修4-4,坐標系與參數方程]
在平面直角坐標系![]() 中,曲線C的參數方程為
中,曲線C的參數方程為![]()
![]() ,以坐標原點為極點,以
,以坐標原點為極點,以![]() 軸正半軸為極軸建立極坐標系,直線
軸正半軸為極軸建立極坐標系,直線![]() 的極坐標方程為
的極坐標方程為![]() 。
。
(1)求直線![]() 的直角坐標方程和曲線C的普通方程。
的直角坐標方程和曲線C的普通方程。
(2)設點P為曲線C上的任意一點,求點P到直線![]() 的距離的最大值。
的距離的最大值。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在平面直角坐標系xOy中,以O為極點,x軸的正半軸為極軸建立極坐標系.若直線l的極坐標方程為![]() ,曲線C的極坐標方程為:
,曲線C的極坐標方程為: ![]() ,將曲線C上所有點的橫坐標縮短為原來的一半,縱坐標不變,然后再向右平移一個單位得到曲線C1.
,將曲線C上所有點的橫坐標縮短為原來的一半,縱坐標不變,然后再向右平移一個單位得到曲線C1.
(1)求曲線C1的直角坐標方程;
(2)已知直線l與曲線C1交于A,B兩點,點P(2,0),求|PA|+|PB|的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某縣政府為了引導居民合理用水,決定全面實施階梯水價,階梯水價原則上以住宅(一套住宅為一戶)的月用水量為基準定價:若用水量不超過12噸時,按4元/噸計算水費;若用水量超過12噸且不超過14噸時,超過12噸部分按6.60元/噸計算水費;若用水量超過14噸時,超過14噸部分按7.80元/噸計算水費.為了了解全市居民月用水量的分布情況,通過抽樣,獲得了100戶居民的月用水量(單位:噸),將數據按照![]() ,
,![]() ,…,
,…,![]() 分成8組,制成了如圖1所示的頻率分布直方圖.
分成8組,制成了如圖1所示的頻率分布直方圖.
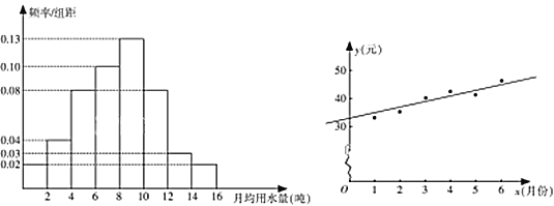
(圖1) (圖2)
(Ⅰ)通過頻率分布直方圖,估計該市居民每月的用水量的平均數和中位數(精確到0.01);
(Ⅱ)求用戶用水費用![]() (元)關于月用水量
(元)關于月用水量![]() (噸)的函數關系式;
(噸)的函數關系式;
(Ⅲ)如圖2是該縣居民李某2017年1~6月份的月用水費![]() (元)與月份
(元)與月份![]() 的散點圖,其擬合的線性回歸方程是
的散點圖,其擬合的線性回歸方程是![]() .若李某2017年1~7月份水費總支出為294.6元,試估計李某7月份的用水噸數.
.若李某2017年1~7月份水費總支出為294.6元,試估計李某7月份的用水噸數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】【2018江西蓮塘一中、臨川二中高三上學期第一次聯考】二次函數![]() 的圖象過原點,對
的圖象過原點,對![]() ,恒有
,恒有![]() 成立,設數列
成立,設數列![]() 滿足
滿足![]() .
.
(I)求證:對![]() ,恒有
,恒有![]() 成立;
成立;
(II)求函數![]() 的表達式;
的表達式;
(III)設數列![]() 前
前![]() 項和為
項和為![]() ,求
,求![]() 的值.
的值.
【答案】(I)證明見解析;(II)![]() ;(III)2018.
;(III)2018.
【解析】試題分析:
(1)左右兩側做差,結合代數式的性質可證得![]() ,即對
,即對![]() ,恒有:
,恒有:![]() 成立;
成立;
(2)由已知條件可設![]() ,給定特殊值,令
,給定特殊值,令![]() ,從而可得:
,從而可得:![]() ,則
,則![]() ,
,![]() ,從而有
,從而有![]() 恒成立,據此可知
恒成立,據此可知![]() ,則
,則![]() .
.
(3)結合(1)(2)的結論整理計算可得:![]() ,據此分組求和有:
,據此分組求和有:![]() .
.
試題解析:
(1)![]() (僅當
(僅當![]() 時,取“=”)
時,取“=”)
所以恒有:![]() 成立;
成立;
(2)由已知條件可設![]() ,則
,則![]() 中,令
中,令![]() ,
,
從而可得:![]() ,所以
,所以![]() ,即
,即![]() ,
,
又因為![]() 恒成立,即
恒成立,即![]() 恒成立,
恒成立,
當![]() 時,
時,![]() ,不合題意舍去,
,不合題意舍去,
當![]() 時,即
時,即![]() ,所以
,所以![]() ,所以
,所以![]() .
.
(3)![]() ,
,
所以![]() ,
,
即![]() .
.
【題型】解答題
【結束】
22
【題目】已知函數![]() 為定義在
為定義在![]() 上的奇函數.
上的奇函數.
(1)求函數![]() 的值域;
的值域;
(2)當![]() 時,不等式
時,不等式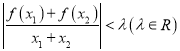 恒成立,求實數
恒成立,求實數![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知三棱柱ABC﹣A1B1C1中,AA1⊥平面ABC,AC=BC,M,N分別是棱CC1,AB的中點.
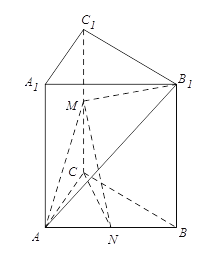
(1)求證:CN⊥平面ABB1A1;
(2)求證:CN∥平面AMB1.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列![]() 中,
中, ![]() ,且
,且![]() 對任意正整數
對任意正整數![]() 都成立,數列
都成立,數列![]() 的前
的前![]() 項和為
項和為![]() .
.
(1)若![]() ,且
,且![]() ,求
,求![]() ;
;
(2)是否存在實數![]() ,使數列
,使數列![]() 是公比為1的等比數列,且任意相鄰三項
是公比為1的等比數列,且任意相鄰三項![]() 按某順序排列后成等差數列,若存在,求出所有
按某順序排列后成等差數列,若存在,求出所有![]() 的值;若不存在,請說明理由;
的值;若不存在,請說明理由;
(3)若![]() ,求
,求![]() .(用
.(用![]() 表示).
表示).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() (m,n為常數),在
(m,n為常數),在![]() 處的切線方程為
處的切線方程為![]() .
.
(Ⅰ)求![]() 的解析式并寫出定義域;
的解析式并寫出定義域;
(Ⅱ)若任意![]() ,使得對任意
,使得對任意![]() 上恒有
上恒有![]() 成立,求實數a的取值范圍;
成立,求實數a的取值范圍;
(Ⅲ)若![]() 有兩個不同的零點
有兩個不同的零點![]() ,求證:
,求證: ![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com