
【題目】(Ⅰ)命題“ ![]() ”為假命題,求實數a的取值范圍;
”為假命題,求實數a的取值范圍;
(Ⅱ)若“x2+2x﹣8<0”是“x﹣m>0”的充分不必要條件,求實數m的取值范圍.
【答案】解:(Ⅰ):x0∈R,x02﹣3ax0+9<0為假命題,等價于x∈R,x2﹣3ax+9≥0為真命題,
∴△=9a2﹣4×9≤0﹣2≤a≤2,
∴實數a的取值范圍是﹣2≤a≤2;
(Ⅱ)由x2+2x﹣8<0﹣4<x<2,
另由x﹣m>0,
即x>m,
∵“x2+2x﹣8<0”是“x﹣m>0”的充分不必要條件,
∴m≤﹣4.
故m的取值范圍是m≤﹣4
【解析】(I)x0∈R,x02﹣3ax0+9<0為假命題,等價于x∈R,x2﹣3ax+9≥0為真命題,利用判別式,即可確定實數a的取值范圍;(II)根據一元二次不等式的解法分別求出兩不等式的解集,由“x2+2x﹣8<0”是“x﹣m>0”的充分不必要條件,可得不等式解集的包含關系,從而求出m的范圍
【考點精析】關于本題考查的特稱命題,需要了解特稱命題![]() :
:![]() ,
,![]() ,它的否定
,它的否定![]() :
:![]() ,
,![]() ;特稱命題的否定是全稱命題才能得出正確答案.
;特稱命題的否定是全稱命題才能得出正確答案.


 舉一反三同步巧講精練系列答案
舉一反三同步巧講精練系列答案 口算與應用題卡系列答案
口算與應用題卡系列答案 名師點睛字詞句段篇系列答案
名師點睛字詞句段篇系列答案科目:高中數學 來源: 題型:
【題目】某校![]() 屆高三文(1)班在一次數學測驗中,全班
屆高三文(1)班在一次數學測驗中,全班![]() 名學生的數學成績的頻率分布直方圖如下,已知分數在
名學生的數學成績的頻率分布直方圖如下,已知分數在![]() 的學生數有
的學生數有![]() 人.
人.
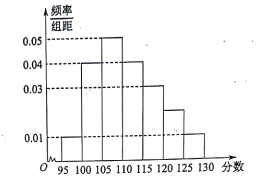
(1)求總人數![]() 和分數在
和分數在![]() 的人數
的人數![]() ;
;
(2)利用頻率分布直方圖,估算該班學生數學成績的眾數和中位數各是多少?
(3)現在從比分數在![]() 名學生(男女生比例為
名學生(男女生比例為![]() )中任選
)中任選![]() 人,求其中至多含有
人,求其中至多含有![]() 名男生的概率.
名男生的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某企業生產A,B兩種產品,根據市場調查與市場預測,A產品的利潤與投資成正比,其關系如圖(1);B產品的利潤與投資的算術平方根成正比,其關系如圖(2)(注:所示圖中的橫坐標表示投資金額,單位為萬元) 
(1)分別求出A,B兩種產品的利潤表示為投資的函數關系式;
(2)該企業已籌集到10萬元資金,并全部投入A,B兩種產品的生產,問:怎樣分配這10萬元資金,才能使企業獲得最大利潤,最大利潤是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若定義在區間D上的函數y=f(x)滿足:對x∈D,M∈R,使得|f(x)|≤M恒成立,則稱函數y=f(x)在區間D上有界.則下列函數中有界的是: .
①y=sinx;② ![]() ;③y=tanx;④
;③y=tanx;④ ![]() ;
;
⑤y=x3+ax2+bx+1(﹣4≤x≤4),其中a,b∈R.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知A、B、C是橢圓M: ![]() =1(a>b>0)上的三點,其中點A的坐標為
=1(a>b>0)上的三點,其中點A的坐標為 ![]() ,BC過橢圓M的中心,且
,BC過橢圓M的中心,且 ![]() .
.
(1)求橢圓M的方程;
(2)過點(0,t)的直線l(斜率存在時)與橢圓M交于兩點P、Q,設D為橢圓M與y軸負半軸的交點,且 ![]() ,求實數t的取值范圍.
,求實數t的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】極坐標與參數方程
在直角坐標系![]() ,直線
,直線![]() 的參數方程是
的參數方程是![]() (
(![]() 為參數).在以
為參數).在以![]() 為極點,
為極點, ![]() 軸正半軸為極軸建立極坐標系中,曲線
軸正半軸為極軸建立極坐標系中,曲線![]() :
: ![]() .
.
(1)當![]() ,
, ![]() 時,判斷直線
時,判斷直線![]() 與曲線
與曲線![]() 的位置關系;
的位置關系;
(2)當![]() 時,若直線與曲
時,若直線與曲![]() 線
線![]() 相交于
相交于![]() ,
, ![]() 兩點,設
兩點,設![]() ,且
,且![]() ,求直線
,求直線![]() 的傾斜角.
的傾斜角.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某學校的平面示意圖為如下圖五邊形區域![]() ,其中三角形區域
,其中三角形區域![]() 為生活區,四邊形區域
為生活區,四邊形區域![]() 為教學區,
為教學區, ![]() 為學校的主要道路(不考慮寬度).
為學校的主要道路(不考慮寬度). ![]() .
.
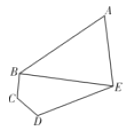
(1)求道路![]() 的長度;(2)求生活區
的長度;(2)求生活區![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com