
【題目】已知![]() 的頂點
的頂點![]() ,
,![]() 邊上的中線
邊上的中線![]() 所在直線方程為
所在直線方程為![]() ,
,![]() 的角平分線
的角平分線![]() 所在直線方程為
所在直線方程為![]() .
.
(I)求頂點![]() 的坐標;
的坐標;
(II)求直線![]() 的方程.
的方程.
【答案】(1)![]() .
.
(2)![]() .
.
【解析】分析:(I)設(shè)頂點![]() 的坐標為
的坐標為![]() ;由頂點
;由頂點![]() 在直線
在直線![]() 上,所以
上,所以![]()
![]()
![]() 在直線
在直線![]() 上, 列方程組求解即可;(II)設(shè)頂點關(guān)于直線
上, 列方程組求解即可;(II)設(shè)頂點關(guān)于直線![]() 的對稱點為
的對稱點為![]() ,根據(jù)中點在對稱軸上,以及直線垂直斜率之積為
,根據(jù)中點在對稱軸上,以及直線垂直斜率之積為![]() ,列方程組求得
,列方程組求得![]() 的值,利用兩點式可得結(jié)果.
的值,利用兩點式可得結(jié)果.
詳解:(I)設(shè)頂點![]() 的坐標為
的坐標為![]() ;
;
因為頂點![]() 在直線
在直線![]() 上,所以
上,所以![]()
由題意知![]() 的坐標為
的坐標為![]() ,
,
因為中點![]() 在直線
在直線![]() 上,所以
上,所以![]() ,
,
即![]() ;
;
聯(lián)立方程組![]() ,解得頂點
,解得頂點![]() 的坐標為
的坐標為![]()
(II)設(shè)頂點關(guān)于直線![]() 的對稱點為
的對稱點為![]() ,
,
由于線段![]() 的中點在在直線
的中點在在直線![]() 上,得方程
上,得方程![]() ,
,
即![]()
由直線![]() 與直線
與直線![]() 垂直,得方程
垂直,得方程![]() ,
,
即![]() ;
;
聯(lián)立方程組![]() ,得
,得![]()
顯然![]() 在直線
在直線![]() 上,且頂點
上,且頂點![]() 的坐標為
的坐標為![]() ,所以直線
,所以直線![]() 的方程為
的方程為![]() ,整理得
,整理得![]() .
.


 口算題卡河北少年兒童出版社系列答案
口算題卡河北少年兒童出版社系列答案 A加金題 系列答案
A加金題 系列答案 全優(yōu)測試卷系列答案
全優(yōu)測試卷系列答案科目:高中數(shù)學 來源: 題型:
【題目】在四棱錐![]() 中,側(cè)面
中,側(cè)面![]() ⊥底面
⊥底面![]() ,底面
,底面![]() 為直角梯形,
為直角梯形,![]() //
//![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 為
為![]() 的中點.
的中點.

(Ⅰ)求證:PA//平面BEF;
(Ⅱ)若PC與AB所成角為![]() ,求
,求![]() 的長;
的長;
(Ⅲ)在(Ⅱ)的條件下,求二面角F-BE-A的余弦值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某農(nóng)科所對冬季晝夜溫差大小與某反季節(jié)大豆新品種發(fā)芽多少之間的關(guān)系進行分析研究,他們分別記錄了![]() 月
月![]() 日至
日至![]() 月
月![]() 日的每天晝夜溫差與實驗室每天每
日的每天晝夜溫差與實驗室每天每![]() 顆種子中的發(fā)芽數(shù),得到如下資料:
顆種子中的發(fā)芽數(shù),得到如下資料:
日期 | 12月1日 | 12月2日 | 12月3日 | 12月4日 | 12月5日 |
溫差 |
|
|
|
|
|
發(fā)芽數(shù) |
|
|
|
|
|
該農(nóng)科所確定的研究方案是:先從這![]() 組數(shù)據(jù)中選取
組數(shù)據(jù)中選取![]() 組,用剩下的
組,用剩下的![]() 組數(shù)據(jù)求線性回歸方程,再用被選取的
組數(shù)據(jù)求線性回歸方程,再用被選取的![]() 組數(shù)據(jù)進行檢驗.
組數(shù)據(jù)進行檢驗.
(1)求選取的![]() 組數(shù)據(jù)恰好是不相鄰
組數(shù)據(jù)恰好是不相鄰![]() 天的數(shù)據(jù)的概率;
天的數(shù)據(jù)的概率;
(2)若選取的是![]() 月
月![]() 日與
日與![]() 月
月![]() 日的兩組數(shù)據(jù),請根據(jù)
日的兩組數(shù)據(jù),請根據(jù)![]() 月
月![]() 日至
日至![]() 日的數(shù)據(jù),求出
日的數(shù)據(jù),求出![]() 關(guān)于
關(guān)于![]() 的線性回歸方程
的線性回歸方程![]() ,由線性回歸方程得到的估計數(shù)據(jù)與所選取的檢驗數(shù)據(jù)的誤差均不超過
,由線性回歸方程得到的估計數(shù)據(jù)與所選取的檢驗數(shù)據(jù)的誤差均不超過![]() 顆,則認為得到的線性回歸方程是可靠的,試問(2)中所得試的線性回歸方程是否可靠?
顆,則認為得到的線性回歸方程是可靠的,試問(2)中所得試的線性回歸方程是否可靠?
附: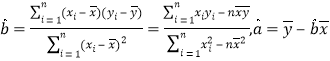
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】用數(shù)學歸納法證明12+22+…+(n﹣1)2+n2+(n﹣1)2+…+22+12═ ![]() 時,由n=k的假設(shè)到證明n=k+1時,等式左邊應(yīng)添加的式子是( )
時,由n=k的假設(shè)到證明n=k+1時,等式左邊應(yīng)添加的式子是( )
A.(k+1)2+2k2
B.(k+1)2+k2
C.(k+1)2
D.![]()
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】(本小題滿分12分)在△ABC中,角A,B,C的對邊分別為a,b,c,C=![]() ,a=5,△ABC的面積為10
,a=5,△ABC的面積為10![]() .
.
(1)求b,c的值;
(2)求cos(B-![]() )的值.
)的值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】甲船在島![]() 的正南方
的正南方![]() 處,
處,![]() 千米,甲船以每小時
千米,甲船以每小時![]() 千米的速度向正北航行,同時乙船自
千米的速度向正北航行,同時乙船自![]() 出發(fā)以每小時
出發(fā)以每小時![]() 千米的速度向北偏東
千米的速度向北偏東![]() 的方向駛?cè)ィ敿祝覂纱嗑嘧罱鼤r,它們所航行的時間是( )
的方向駛?cè)ィ敿祝覂纱嗑嘧罱鼤r,它們所航行的時間是( )
A. ![]() 分鐘 B.
分鐘 B. ![]() 分鐘 C.
分鐘 C. ![]() 分鐘 D.
分鐘 D. ![]() 分鐘
分鐘
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com