
【題目】如圖,在四棱錐![]() 中,已知
中,已知![]() 底面
底面![]() ,異面直線
,異面直線![]() 和
和![]() 所成角等于
所成角等于![]() .
.
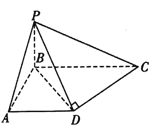
(1)求證: 平面![]() 平面
平面![]() ;
;
(2)求直線![]() 和平面
和平面![]() 所成角的正弦值;
所成角的正弦值;
(3) 在棱![]() 上是否存在一點
上是否存在一點![]() ,使得平面
,使得平面![]() 與平面
與平面![]() 所成銳二面角的正切值為
所成銳二面角的正切值為![]() ?若存在,指出點
?若存在,指出點![]() 在棱
在棱![]() 上的位置,若不存在,說明理由.
上的位置,若不存在,說明理由.
【答案】(1)見解析;(2)![]() ;(3)存在這樣的
;(3)存在這樣的![]() 點,
點, ![]() 為棱
為棱![]() 上靠近
上靠近![]() 的三等分點.
的三等分點.
【解析】試題分析:(1)要證平面![]() 平面
平面![]() ,即證
,即證![]() 平面
平面![]() ;
;
(2)以為![]() 原點,
原點, ![]() 所在直線分別為
所在直線分別為![]() 軸,建立空間直角坐標系,求面
軸,建立空間直角坐標系,求面![]() 的法向量,利用向量求線面角即可;
的法向量,利用向量求線面角即可;
(3)假設(shè)存在,設(shè)![]() ,利用法向量求平面
,利用法向量求平面![]() 與平面
與平面![]() 所成角即可.
所成角即可.
試題解析:
(1) ![]() 底面
底面![]() ,又
,又![]() 平面
平面![]() 平面
平面![]() 平面
平面![]() ,
, ![]() 平面
平面![]() 平面
平面![]() .
.

(2)如圖,以為![]() 原點,
原點, ![]() 所在直線分別為
所在直線分別為![]() 軸,建立空間直角坐標系,由(1)易知
軸,建立空間直角坐標系,由(1)易知![]() 是等腰直角三角形,
是等腰直角三角形, ![]() .設(shè)
.設(shè)![]() ,則
,則![]() ,則
,則![]() ,因為異面直線
,因為異面直線![]() 和
和![]() 所成角等于
所成角等于![]() ,
, 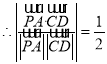 ,即
,即![]() ,解得
,解得![]() .設(shè)平面
.設(shè)平面![]() 的一個法向量為
的一個法向量為![]() ,則由
,則由 ,得
,得![]() ,所以可取
,所以可取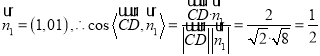 ,所以直線
,所以直線![]() 和平面
和平面![]() 所成的正弦值為
所成的正弦值為![]() .
.
(3)假設(shè)存在,設(shè)![]() ,且
,且![]() ,則
,則![]() ,設(shè)平面
,設(shè)平面![]() 一個法向量為
一個法向量為![]() ,則由
,則由 ,得
,得![]() ,取
,取![]() ,又平面
,又平面![]() 的法向量為
的法向量為![]() ,由平面
,由平面![]() 與平面
與平面![]() 所成銳二面角的正切值為
所成銳二面角的正切值為![]() ,可知余弦值為
,可知余弦值為![]() ,由
,由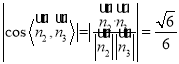 ,解得
,解得![]() 或
或![]() (不合題意).
(不合題意).
所以存在這樣的![]() 點,
點, ![]() 為棱
為棱![]() 上靠近
上靠近![]() 的三等分點.
的三等分點.


科目:高中數(shù)學 來源: 題型:
【題目】已知橢圓C: ![]() (a>b>0)的離心率為
(a>b>0)的離心率為![]() ,以原點O為圓心,橢圓的短半軸長為半徑的圓與直線x﹣y+
,以原點O為圓心,橢圓的短半軸長為半徑的圓與直線x﹣y+![]() =0相切.
=0相切.
(Ⅰ)求橢圓C的標準方程;
(Ⅱ)若直線l:y=kx+m與橢圓C相交于A、B兩點,且kOAkOB=﹣![]() ,判斷△AOB的面積是否為定值?若為定值,求出定值;若不為定值,說明理由.
,判斷△AOB的面積是否為定值?若為定值,求出定值;若不為定值,說明理由.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知三角形△ABC的三邊長構(gòu)成公差為2的等差數(shù)列,且最大角的正弦值為 ![]() ,則這個三角形的周長為( )
,則這個三角形的周長為( )
A.15
B.18
C.21
D.24
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】根據(jù)國家環(huán)保部新修訂的《環(huán)境空氣質(zhì)量標準》規(guī)定:居民區(qū)![]() 的年平均濃度不得超過35微克/立方米,
的年平均濃度不得超過35微克/立方米, ![]() 的24小時平均濃度不得超過75微克/立方米.我市環(huán)保局隨機抽取了一居民區(qū)2016年30天
的24小時平均濃度不得超過75微克/立方米.我市環(huán)保局隨機抽取了一居民區(qū)2016年30天![]() 的24小時平均濃度(單位:微克/立方米)的監(jiān)測數(shù)據(jù),將這30天的測量結(jié)果繪制成樣本頻率分布直方圖如圖.
的24小時平均濃度(單位:微克/立方米)的監(jiān)測數(shù)據(jù),將這30天的測量結(jié)果繪制成樣本頻率分布直方圖如圖.
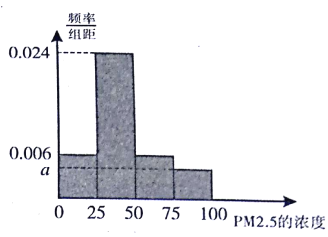
(Ⅰ)求圖中![]() 的值;
的值;
(Ⅱ)由頻率分布直方圖中估算樣本平均數(shù),并根據(jù)樣本估計總體的思想,從![]() 的年平均濃度考慮,判斷該居民區(qū)的環(huán)境質(zhì)量是否需要改善?并說明理由.
的年平均濃度考慮,判斷該居民區(qū)的環(huán)境質(zhì)量是否需要改善?并說明理由.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知數(shù)列{an}的前n項和為Sn , 且Sn=n﹣5an﹣85,n∈N+ .
(1)求an .
(2)求數(shù)列{Sn}的通項公式,并求出n為何值時,Sn取得最小值?并說明理由.(參考數(shù)據(jù):lg 2≈0.3,lg 3≈0.48).
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某教育機構(gòu)隨機某校20個班級,調(diào)查各班關(guān)注漢字聽寫大賽的學生人數(shù),根據(jù)所得數(shù)據(jù)的莖葉圖,以組距為5將數(shù)據(jù)分組成[0,5),[5,10),[10,15),[15,20),[20,25),[25,30),[30,35),[35,40]時,所作的頻率分布直方圖如圖所示,則原始莖葉圖可能是( ) 
A.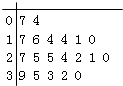
B.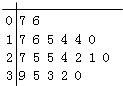
C.
D.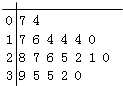
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某顏料公司生產(chǎn)![]() 、
、![]() 兩種產(chǎn)品,其中生產(chǎn)每噸
兩種產(chǎn)品,其中生產(chǎn)每噸![]() 產(chǎn)品,需要甲染料
產(chǎn)品,需要甲染料![]() 噸,乙染料
噸,乙染料![]() 噸,丙染料
噸,丙染料![]() 噸,生產(chǎn)每噸
噸,生產(chǎn)每噸![]() 產(chǎn)品,需要甲染料
產(chǎn)品,需要甲染料![]() 噸,乙染料
噸,乙染料![]() 噸,丙染料
噸,丙染料![]() 噸,且該公司一天之內(nèi)甲、乙、丙三種染料的用量分別不超過
噸,且該公司一天之內(nèi)甲、乙、丙三種染料的用量分別不超過![]() 噸、
噸、![]() 噸、
噸、![]() 噸,如果
噸,如果![]() 產(chǎn)品的利潤為
產(chǎn)品的利潤為![]() 元/噸,
元/噸, ![]() 產(chǎn)品的利潤為
產(chǎn)品的利潤為![]() 元/噸,則該顏料公司一天內(nèi)可獲得的最大利潤為( )
元/噸,則該顏料公司一天內(nèi)可獲得的最大利潤為( )
A. ![]() 元 B.
元 B. ![]() 元 C.
元 C. ![]() 元 D.
元 D. ![]() 元
元
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() ,其中
,其中![]() 為自然對數(shù)的底數(shù).
為自然對數(shù)的底數(shù).
(1)當![]() 時,討論函數(shù)
時,討論函數(shù)![]() 的單調(diào)性;
的單調(diào)性;
(2)當![]() 時,求證:對任意的
時,求證:對任意的![]() .
.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com