
【題目】已知函數(shù)![]() (其中
(其中![]() )的圖象上相鄰兩個最高點的距離為
)的圖象上相鄰兩個最高點的距離為![]() .
.
(1)求函數(shù)![]() 的圖象的所有對稱軸;
的圖象的所有對稱軸;
(2)若函數(shù)![]() 在
在![]() 內(nèi)有兩個零點
內(nèi)有兩個零點![]() 、
、![]() ,求
,求![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() ;(2)
;(2)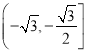 .
.
【解析】
(1)根據(jù)題中條件可得出函數(shù)![]() 的最小正周期,可計算出
的最小正周期,可計算出![]() 的值,令
的值,令![]() ,可得出函數(shù)
,可得出函數(shù)![]() 的圖象的對稱軸方程;
的圖象的對稱軸方程;
(2)由![]() ,可得出
,可得出![]() ,令
,令![]() ,則問題可以轉化為直線
,則問題可以轉化為直線![]() 與函數(shù)
與函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上的圖象有兩個交點,利用數(shù)形結合思想可得出實數(shù)
上的圖象有兩個交點,利用數(shù)形結合思想可得出實數(shù)![]() 的取值范圍.
的取值范圍.
(1)因為![]() 的圖象上相鄰兩個最高點的距離為
的圖象上相鄰兩個最高點的距離為![]() ,則該函數(shù)的最小正周期為
,則該函數(shù)的最小正周期為![]() ,
,![]() ,
,
所以,![]() .
.
令![]() ,解得
,解得![]() ,
,
因此,函數(shù)![]() 的圖象的所有對稱軸的方程為
的圖象的所有對稱軸的方程為![]() ;
;
(2)由![]() ,可得出
,可得出![]() ,
,
令![]() ,當
,當![]() 時,
時,![]() ,
,
則直線![]() 與函數(shù)
與函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上的圖象有兩個交點,如下圖所示:
上的圖象有兩個交點,如下圖所示:

由圖象知,當 時,直線
時,直線![]() 與函數(shù)
與函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上的圖象有兩個交點.
上的圖象有兩個交點.
因此,實數(shù)![]() 的取值范圍是
的取值范圍是 .
.


 奪冠金卷全能練考系列答案
奪冠金卷全能練考系列答案科目:高中數(shù)學 來源: 題型:
【題目】當前,以“立德樹人”為目標的課程改革正在有序推進.高中聯(lián)招對初三畢業(yè)學生進行體育測試,是激發(fā)學生、家長和學校積極開展體育活動,保證學生健康成長的有效措施.程度2019年初中畢業(yè)生升學體育考試規(guī)定,考生必須參加立定跳遠、擲實心球、1分鐘跳繩三項測試,三項考試滿分50分,其中立定跳遠15分,擲實心球15分,1分鐘跳繩20分.某學校在初三上期開始時要掌握全年級學生每分鐘跳繩的情況,隨機抽取了100名學生進行測試,得到下邊頻率分布直方圖,且規(guī)定計分規(guī)則如下表:
每分鐘跳繩個數(shù) |
|
|
|
|
得分 | 17 | 18 | 19 | 20 |
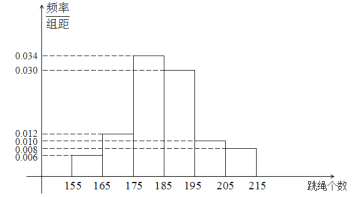
(Ⅰ)現(xiàn)從樣本的100名學生中,任意選取2人,求兩人得分之和不大于35分的概率;;
(Ⅱ)若該校初三年級所有學生的跳繩個數(shù)![]() 服從正態(tài)分布
服從正態(tài)分布![]() ,用樣本數(shù)據(jù)的平均值和方差估計總體的期望和方差,已知樣本方差
,用樣本數(shù)據(jù)的平均值和方差估計總體的期望和方差,已知樣本方差![]() (各組數(shù)據(jù)用中點值代替).根據(jù)往年經(jīng)驗,該校初三年級學生經(jīng)過一年的訓練,正式測試時每人每分鐘跳繩個數(shù)都有明顯進步,假設今年正式測試時每人每分鐘跳繩個數(shù)比初三上學期開始時個數(shù)增加10個,現(xiàn)利用所得正態(tài)分布模型:
(各組數(shù)據(jù)用中點值代替).根據(jù)往年經(jīng)驗,該校初三年級學生經(jīng)過一年的訓練,正式測試時每人每分鐘跳繩個數(shù)都有明顯進步,假設今年正式測試時每人每分鐘跳繩個數(shù)比初三上學期開始時個數(shù)增加10個,現(xiàn)利用所得正態(tài)分布模型:
![]() 預計全年級恰有2000名學生,正式測試每分鐘跳182個以上的人數(shù);(結果四舍五入到整數(shù))
預計全年級恰有2000名學生,正式測試每分鐘跳182個以上的人數(shù);(結果四舍五入到整數(shù))
![]() 若在全年級所有學生中任意選取3人,記正式測試時每分鐘跳195以上的人數(shù)為ξ,求隨機變量的分布列和期望.
若在全年級所有學生中任意選取3人,記正式測試時每分鐘跳195以上的人數(shù)為ξ,求隨機變量的分布列和期望.
附:若隨機變量![]() 服從正態(tài)分布
服從正態(tài)分布![]() ,則
,則![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
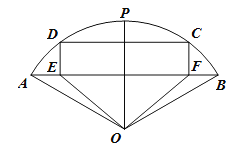
【題目】有一塊圓心角為120度,半徑為![]() 的扇形鋼板
的扇形鋼板![]() (
(![]() 為弧
為弧![]() 的中點),現(xiàn)要將其裁剪成一個五邊形磨具
的中點),現(xiàn)要將其裁剪成一個五邊形磨具![]() ,其下部為等腰三角形
,其下部為等腰三角形![]() ,上部為矩形
,上部為矩形![]() .設
.設![]() 五邊形
五邊形![]() 的面積為
的面積為![]() .
.
(1)寫出![]() 關于
關于![]() 的函數(shù)表達式,并寫出
的函數(shù)表達式,并寫出![]() 的取值范圍;
的取值范圍;
(2)當![]() 取得最大值時,求
取得最大值時,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
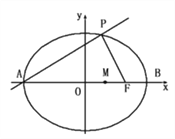
【題目】如圖,A、B分別是橢圓![]() 的左、右端點,F是橢圓的右焦點,點P在橢圓上,且位于x軸上方,PA⊥PF.
的左、右端點,F是橢圓的右焦點,點P在橢圓上,且位于x軸上方,PA⊥PF.
(1)點P的坐標;
(2)設M是橢圓長軸AB上的一點,M到直線AP的距離等于MB,求橢圓上的點到點M的距離d的最小值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某連鎖經(jīng)營公司所屬5個零售店某月的銷售額和利潤額資料如下表
商店名稱 | A | B | C | D | E |
銷售額x(千萬元) | 3 | 5 | 6 | 7 | 9 |
利潤額y(百萬元) | 2 | 3 | 3 | 4 | 5 |
(1)畫出散點圖.觀察散點圖,說明兩個變量有怎樣的相關性.

(2)用最小二乘法計算利潤額y對銷售額x的回歸直線方程.
(3)當銷售額為4(千萬元)時,估計利潤額的大小.
其中
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,在長方形ABCD中,AB=![]() ,AD=2,E,F為線段AB的三等分點,G、H為線段DC的三等分點.將長方形ABCD卷成以AD為母線的圓柱W的半個側面,AB、CD分別為圓柱W上、下底面的直徑.
,AD=2,E,F為線段AB的三等分點,G、H為線段DC的三等分點.將長方形ABCD卷成以AD為母線的圓柱W的半個側面,AB、CD分別為圓柱W上、下底面的直徑.

(Ⅰ)證明:平面ADHF⊥平面BCHF;
(Ⅱ)若P為DC的中點,求三棱錐H—AGP的體積.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】中國高鐵的快速發(fā)展給群眾出行帶來巨大便利,極大促進了區(qū)域經(jīng)濟社會發(fā)展.已知某條高鐵線路通車后,發(fā)車時間間隔![]() (單位:分鐘)滿足
(單位:分鐘)滿足![]() ,經(jīng)測算,高鐵的載客量與發(fā)車時間間隔
,經(jīng)測算,高鐵的載客量與發(fā)車時間間隔![]() 相關:當
相關:當![]() 時高鐵為滿載狀態(tài),載客量為
時高鐵為滿載狀態(tài),載客量為![]() 人;當
人;當![]() 時,載客量會在滿載基礎上減少,減少的人數(shù)與
時,載客量會在滿載基礎上減少,減少的人數(shù)與![]() 成正比,且發(fā)車時間間隔為
成正比,且發(fā)車時間間隔為![]() 分鐘時的載客量為
分鐘時的載客量為![]() 人.記發(fā)車間隔為
人.記發(fā)車間隔為![]() 分鐘時,高鐵載客量為
分鐘時,高鐵載客量為![]() .
.
![]() 求
求![]() 的表達式;
的表達式;
![]() 若該線路發(fā)車時間間隔為
若該線路發(fā)車時間間隔為![]() 分鐘時的凈收益
分鐘時的凈收益![]() (元),當發(fā)車時間間隔為多少時,單位時間的凈收益
(元),當發(fā)車時間間隔為多少時,單位時間的凈收益![]() 最大?
最大?
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知直線l方程為(m+2)x﹣(m+1)y﹣3m﹣7=0,m∈R.
(1)求證:直線l恒過定點P,并求出定點P的坐標;
(2)若直線l在x軸,y軸上的截距相等,求直線l的方程.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com