
【題目】如圖,在三棱錐![]() 中,
中,![]() ,
,![]() ,
,![]() 為
為![]() 的中點.
的中點.
(1)證明:![]() 平面
平面![]() ;
;
(2)若點![]() 在棱
在棱![]() 上,且
上,且![]() ,求點
,求點![]() 到平面
到平面![]() 的距離.
的距離.

【答案】解:
(1)因為AP=CP=AC=4,O為AC的中點,所以OP⊥AC,且OP=![]() .
.
連結(jié)OB.因為AB=BC=![]() ,所以△ABC為等腰直角三角形,且OB⊥AC,OB=
,所以△ABC為等腰直角三角形,且OB⊥AC,OB=![]() =2.
=2.
由![]() 知,OP⊥OB.
知,OP⊥OB.
由OP⊥OB,OP⊥AC知PO⊥平面ABC.
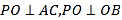
(2)作CH⊥OM,垂足為H.又由(1)可得OP⊥CH,所以CH⊥平面POM.
故CH的長為點C到平面POM的距離.
由題設(shè)可知OC=![]() =2,CM=
=2,CM=![]() =
=![]() ,∠ACB=45°.
,∠ACB=45°.
所以OM=![]() ,CH=
,CH=![]() =
=![]() .
.
所以點C到平面POM的距離為![]() .
.
【解析】分析:(1)連接![]() ,欲證
,欲證![]() 平面
平面![]() ,只需證明
,只需證明![]() 即可;(2)過點
即可;(2)過點![]() 作
作![]() ,垂足為
,垂足為![]() ,只需論證
,只需論證![]() 的長即為所求,再利用平面幾何知識求解即可.
的長即為所求,再利用平面幾何知識求解即可.
詳解:(1)因為AP=CP=AC=4,O為AC的中點,所以OP⊥AC,且OP=![]() .
.
連結(jié)OB.因為AB=BC=![]() ,所以△ABC為等腰直角三角形,且OB⊥AC,OB=
,所以△ABC為等腰直角三角形,且OB⊥AC,OB=![]() =2.
=2.
由![]() 知,OP⊥OB.
知,OP⊥OB.
由OP⊥OB,OP⊥AC知PO⊥平面ABC.
(2)作CH⊥OM,垂足為H.又由(1)可得OP⊥CH,所以CH⊥平面POM.
故CH的長為點C到平面POM的距離.
由題設(shè)可知OC=![]() =2,CM=
=2,CM=![]() =
=![]() ,∠ACB=45°.
,∠ACB=45°.
所以OM=![]() ,CH=
,CH=![]() =
=![]() .
.
所以點C到平面POM的距離為![]() .
.


 字詞句篇與同步作文達標系列答案
字詞句篇與同步作文達標系列答案科目:高中數(shù)學 來源: 題型:
【題目】設(shè)函數(shù)![]() 的解析式滿足
的解析式滿足![]() .
.
(1)求函數(shù)![]() 的解析式;
的解析式;
(2)若![]() 在區(qū)間(1,+∞)單調(diào)遞增,求
在區(qū)間(1,+∞)單調(diào)遞增,求![]() 的取值范圍(只需寫出范圍,不用說明理由)。
的取值范圍(只需寫出范圍,不用說明理由)。
(3)當![]() 時,記函數(shù)
時,記函數(shù)![]() ,求函數(shù)g(x)在區(qū)間
,求函數(shù)g(x)在區(qū)間![]() 上的值域.
上的值域.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在平面直角坐標系xOy中,F(xiàn)是拋物線C:x2=2py(p>0)的焦點,M是拋物線C上位于第一象限內(nèi)的任意一點,過M,F(xiàn),O三點的圓的圓心為Q,點Q到拋物線C的準線的距離為 ![]() .
.
(1)求拋物線C的方程;
(2)是否存在點M,使得直線MQ與拋物線C相切于點M?若存在,求出點M的坐標;若不存在,說明理由;
(3)若點M的橫坐標為 ![]() ,直線l:y=kx+
,直線l:y=kx+ ![]() 與拋物線C有兩個不同的交點A,B,l與圓Q有兩個不同的交點D,E,求當
與拋物線C有兩個不同的交點A,B,l與圓Q有兩個不同的交點D,E,求當 ![]() ≤k≤2時,|AB|2+|DE|2的最小值.
≤k≤2時,|AB|2+|DE|2的最小值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上的最小值記為
上的最小值記為![]() .
.
(1)當![]() 時,求函數(shù)
時,求函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上的值域;
上的值域;
(2)求![]() 的函數(shù)表達式;
的函數(shù)表達式;
(3)求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在直角坐標系![]() 中,曲線
中,曲線![]() 的參數(shù)方程是
的參數(shù)方程是 (
(![]() 為參數(shù)),以該直角坐標系的原點
為參數(shù)),以該直角坐標系的原點![]() 為極點,
為極點, ![]() 軸的正半軸為極軸建立極坐標系,直線
軸的正半軸為極軸建立極坐標系,直線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)寫出曲線![]() 的普通方程和直線
的普通方程和直線![]() 的直角坐標方程;
的直角坐標方程;
(2)設(shè)點![]() ,直線
,直線![]() 與曲線
與曲線![]() 相交于
相交于![]() 兩點,且
兩點,且![]() ,求實數(shù)
,求實數(shù)![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() .
.
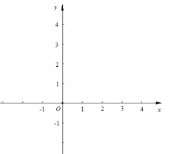
(1)請在所給的平面直角坐標系中畫出函數(shù)![]() 的圖象;
的圖象;
(2)根據(jù)函數(shù)![]() 的圖象回答下列問題:①求函數(shù)
的圖象回答下列問題:①求函數(shù)![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
②求函數(shù)![]() 的值域;③求關(guān)于
的值域;③求關(guān)于![]() 的方程
的方程![]() 在區(qū)間
在區(qū)間![]() 上解的個數(shù).(回答上述3個小題都只需直接寫出結(jié)果,不需給出演算步驟)
上解的個數(shù).(回答上述3個小題都只需直接寫出結(jié)果,不需給出演算步驟)
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在邊長是2的正方體ABCD﹣A1B1C1D1中,E,F(xiàn)分別為AB,A1C的中點.應(yīng)用空間向量方法求解下列問題. 
(1)求EF的長
(2)證明:EF∥平面AA1D1D;
(3)證明:EF⊥平面A1CD.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在用二次法求方程3x+3x-8=0在(1,2)內(nèi)近似根的過程中,已經(jīng)得到f(1)<0,f(1.5)>0,f(1.25)<0,則方程的根落在區(qū)間( )
A. ![]() B.
B. ![]() C.
C. ![]() D. 不能確定
D. 不能確定
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com