
【題目】在所有棱長都相等的三棱錐![]() 中,D,E,F分別是AB,BC,CA的中點,下列四個命題:
中,D,E,F分別是AB,BC,CA的中點,下列四個命題:
(1)![]() 平面PDF;(2)
平面PDF;(2)![]() 平面
平面![]() ;
;
(3)平面![]() 平面
平面![]() ;(4)平面
;(4)平面![]() 平面
平面![]() .
.
其中正確命題的序號為________.
A.(2)(3)B.(1)(3)C.(2)(4)D.(1)(4)
【答案】C
【解析】
(1)根據(jù)三角形中位線得![]() ,根據(jù)線面平行判定定理可知(1)正確;
,根據(jù)線面平行判定定理可知(1)正確;
(2)根據(jù)位置關(guān)系可知![]() 與平面
與平面![]() 相交,(2)錯誤;
相交,(2)錯誤;
(3)假設(shè)垂直關(guān)系成立,根據(jù)面面垂直的性質(zhì)可證得![]() 平面
平面![]() ,由線面垂直性質(zhì)得到
,由線面垂直性質(zhì)得到![]() ,根據(jù)等腰三角形三線合一可得
,根據(jù)等腰三角形三線合一可得![]() ,則
,則![]() ,不成立可知假設(shè)錯誤,故(3)錯誤;
,不成立可知假設(shè)錯誤,故(3)錯誤;
(4)根據(jù)線面垂直的判定定理可證得![]() 平面
平面![]() ,由面面垂直判定定理可證得結(jié)論,知(4)正確.
,由面面垂直判定定理可證得結(jié)論,知(4)正確.
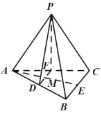
(1)![]() 分別為
分別為![]() 中點
中點 ![]()
![]() 平面
平面![]() ,
,![]() 平面
平面![]()
![]() 平面
平面![]() ,(1)正確;
,(1)正確;
(2)![]() ,
,![]() 平面
平面![]()
![]() 平面
平面![]() ,(2)正確;
,(2)正確;
(3)假設(shè)平面![]() 平面
平面![]()
![]()
![]() ,
,![]() 為
為![]() 中點
中點 ![]() ,又
,又![]()
![]()
![]() 平面
平面![]() 平面
平面![]() ,
,![]() 平面
平面![]()
![]() 平面
平面![]()
![]() 平面
平面![]()
![]()
![]() ,
,![]() 為
為![]() 中點
中點 ![]()
![]() ,顯然不成立
,顯然不成立
故假設(shè)錯誤,(3)錯誤;
(4)![]() 三棱錐所有棱長都相等
三棱錐所有棱長都相等 ![]()
又![]() ,
,![]() 為
為![]() 中點
中點 ![]() ,
,![]()
![]() 平面
平面![]() ,
,![]()
![]() 平面
平面![]()
又![]() 平面
平面![]()
![]() 平面
平面![]() 平面
平面![]() ,(4)正確
,(4)正確


 同步奧數(shù)系列答案
同步奧數(shù)系列答案科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() :
:![]() 的左,右焦點分別為
的左,右焦點分別為![]() ,
,![]() ,點
,點![]() 為橢圓
為橢圓![]() 上任意一點,點
上任意一點,點![]() 關(guān)于原點
關(guān)于原點![]() 的對稱點為點
的對稱點為點![]() ,有
,有![]() ,且當(dāng)
,且當(dāng)![]() 的面積最大時為等邊三角形.
的面積最大時為等邊三角形.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)與圓![]() 相切的直線
相切的直線![]() :
:![]() 交橢圓
交橢圓![]() 于
于![]() ,
,![]() 兩點,若橢圓上存在點
兩點,若橢圓上存在點![]() 滿足
滿足![]() ,求四邊形
,求四邊形![]() 面積的取值范圍.
面積的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】《中華人民共和國道路交通安全法》第47條的相關(guān)規(guī)定:機動車行經(jīng)人行橫道時,應(yīng)當(dāng)減速慢行;遇行人正在通過人行橫道,應(yīng)當(dāng)停車讓行,俗稱“禮讓斑馬線”,《中華人民共和國道路交通安全法》第90條規(guī)定:對不禮讓行人的駕駛員處以扣3分,罰款50元的處罰.
(1)交警從這5個月內(nèi)通過該路口的駕駛員中隨機抽查了50人,調(diào)查駕駛員不“禮讓斑馬線”行為與駕齡的關(guān)系,得到如下列聯(lián)表:能否據(jù)此判斷有97.5%的把握認為“禮讓斑馬線”行為與駕齡有關(guān)?
不禮讓斑馬線 | 禮讓斑馬線 | 合計 | |
駕齡不超過1年 | 22 | 8 | 30 |
駕齡1年以上 | 8 | 12 | 20 |
合計 | 30 | 20 | 50 |
(2)下圖是某市一主干路口監(jiān)控設(shè)備所抓拍的5個月內(nèi)駕駛員不“禮讓斑馬線”行為的折線圖:
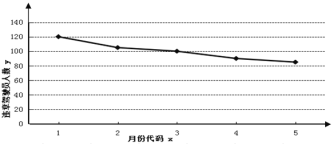
請結(jié)合圖形和所給數(shù)據(jù)求違章駕駛員人數(shù)y與月份x之間的回歸直線方程![]() ,并預(yù)測該路口7月份的不“禮讓斑馬線”違章駕駛員人數(shù).
,并預(yù)測該路口7月份的不“禮讓斑馬線”違章駕駛員人數(shù).
附注:參考數(shù)據(jù):![]() ,
,![]() .
.
參考公式: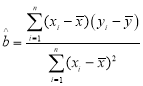 ,
,![]() ,
,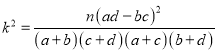 (其中
(其中![]() )
)
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在所有棱長都相等的三棱錐![]() 中,D,E,F分別是AB,BC,CA的中點,下列四個命題:
中,D,E,F分別是AB,BC,CA的中點,下列四個命題:
(1)![]() 平面PDF;(2)
平面PDF;(2)![]() 平面
平面![]() ;
;
(3)平面![]() 平面
平面![]() ;(4)平面
;(4)平面![]() 平面
平面![]() .
.
其中正確命題的序號為________.
A.(2)(3)B.(1)(3)C.(2)(4)D.(1)(4)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() .
.
(Ⅰ)求曲線![]() 在點
在點![]() 處的切線方程;
處的切線方程;
(Ⅱ)若函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上存在極值,求實數(shù)
上存在極值,求實數(shù)![]() 的取值范圍;
的取值范圍;
(Ⅲ)設(shè)![]() ,對任意
,對任意![]() 恒有
恒有![]() ,求實數(shù)
,求實數(shù)![]() 的取值范圍。
的取值范圍。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
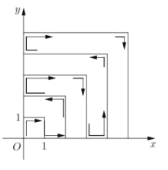
【題目】如圖,一個粒子從原點出發(fā),在第一象限和兩坐標軸正半軸上運動,在第一秒時它從原點運動到點![]() ,接著它按圖所示在
,接著它按圖所示在![]() 軸、
軸、![]() 軸的垂直方向上來回運動,且每秒移動一個單位長度,那么,在2018秒時,這個粒子所處的位置在點______.
軸的垂直方向上來回運動,且每秒移動一個單位長度,那么,在2018秒時,這個粒子所處的位置在點______.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在極坐標系下,方程![]() 的圖形為如圖所示的“幸運四葉草”,又稱為玫瑰線.
的圖形為如圖所示的“幸運四葉草”,又稱為玫瑰線.

(1)當(dāng)玫瑰線的![]() 時,求以極點為圓心的單位圓與玫瑰線的交點的極坐標;
時,求以極點為圓心的單位圓與玫瑰線的交點的極坐標;
(2)求曲線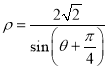 上的點M與玫瑰線上的點N距離的最小值及取得最小值時的點M、N的極坐標(不必寫詳細解題過程).
上的點M與玫瑰線上的點N距離的最小值及取得最小值時的點M、N的極坐標(不必寫詳細解題過程).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已定義![]() ,已知函數(shù)
,已知函數(shù)![]() 的定義域都是
的定義域都是![]() ,則下列四個命題中為真命題的是_________.(寫出所有真命題的序號)
,則下列四個命題中為真命題的是_________.(寫出所有真命題的序號)
① 若![]() 都是奇函數(shù),則函數(shù)
都是奇函數(shù),則函數(shù)![]() 為奇函數(shù).
為奇函數(shù).
② 若![]() 都是偶函數(shù),則函數(shù)
都是偶函數(shù),則函數(shù)![]() 為偶函數(shù).
為偶函數(shù).
③ 若![]() 都是增函數(shù),則函數(shù)
都是增函數(shù),則函數(shù)![]() 為增函數(shù).
為增函數(shù).
④ 若![]() 都是減函數(shù),則函數(shù)
都是減函數(shù),則函數(shù)![]() 為減函數(shù).
為減函數(shù).
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com