
【題目】如圖,![]() 是正方形ABCD的外接圓,點(diǎn)P在劣弧AB上(P不與A、B重合),DP分別交AO、AB于點(diǎn)Q、T,
是正方形ABCD的外接圓,點(diǎn)P在劣弧AB上(P不與A、B重合),DP分別交AO、AB于點(diǎn)Q、T, ![]() 在點(diǎn)P處的切線交DA的延長(zhǎng)線于點(diǎn)E,劣弧BC的中點(diǎn)為F.
在點(diǎn)P處的切線交DA的延長(zhǎng)線于點(diǎn)E,劣弧BC的中點(diǎn)為F.

(1)問:何時(shí)F、T、E三點(diǎn)共線?請(qǐng)說明理由.
(2)求比值![]() 的取值范圍.
的取值范圍.
【答案】(1)見解析;(2)![]()
【解析】
(1)如圖,不妨設(shè)正方形![]() 的邊長(zhǎng)為1,記
的邊長(zhǎng)為1,記![]() .則
.則
![]()
![]() .
.
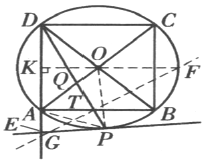
設(shè)直線FO交AD于點(diǎn)K.則
![]() .
.
又EP 切![]() 于P,由弦切角定理得
于P,由弦切角定理得
![]() .
.
因?yàn)椤螪PA=∠DBA=45°,所以
![]() ,
,
![]() .
.
由正弦定理得
![]() ,
,
![]() .
.
設(shè)直線FT交直線DA于點(diǎn)G.
由![]() 得
得![]() ,則
,則![]() .
.
故![]() .
.
下面證明:![]() ,從而
,從而![]() 與
與![]() 不重合,即F、T、E三點(diǎn)不可能共線.
不重合,即F、T、E三點(diǎn)不可能共線.
![]()
![]()
![]()
(由![]() 的取值知
的取值知![]() )
)
![]()
![]()
![]()
![]()
![]()
![]()
上式顯然成立.
故![]() 三點(diǎn)不可能共線.
三點(diǎn)不可能共線.
(2)由正弦定理得
![]() ,
,
![]() ,
,
及![]() ,
,
即![]() .于是,
.于是,
![]()
![]()
![]()
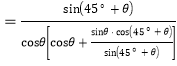
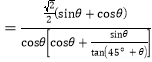
![]()
![]()
![]()
![]() .
.
顯然,![]() 和
和![]() .
.
均為大于0的嚴(yán)格遞增函數(shù),因此,![]() 是關(guān)于變量
是關(guān)于變量![]() 的大于0的嚴(yán)格遞增函數(shù),所以,
的大于0的嚴(yán)格遞增函數(shù),所以,![]() 的值域是
的值域是![]() .
.


 暑假作業(yè)海燕出版社系列答案
暑假作業(yè)海燕出版社系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在邊長(zhǎng)為![]() 的菱形
的菱形![]() 中,
中,![]() .點(diǎn)
.點(diǎn)![]() ,
,![]() 分別在邊
分別在邊![]() ,
,![]() 上,點(diǎn)
上,點(diǎn)![]() 與點(diǎn)
與點(diǎn)![]() ,
,![]() 不重合,
不重合,![]() ,
,![]() .沿
.沿![]() 將
將![]() 翻折到
翻折到![]() 的位置,使平面
的位置,使平面![]() 平面
平面![]() .
.

(1)求證:![]() 平面
平面![]() ;
;
(2)當(dāng)![]() 與平面
與平面![]() 所成的角為
所成的角為![]() 時(shí),求平面
時(shí),求平面![]() 與平面
與平面![]() 所成銳二面角的余弦值.
所成銳二面角的余弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,短軸長(zhǎng)為4.
,短軸長(zhǎng)為4.
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)過點(diǎn)![]() 作兩條直線,分別交橢圓
作兩條直線,分別交橢圓![]() 于
于![]() ,
,![]() 兩點(diǎn)(異于
兩點(diǎn)(異于![]() 點(diǎn)).當(dāng)直線
點(diǎn)).當(dāng)直線![]() ,
,![]() 的斜率之和為定值
的斜率之和為定值![]() 時(shí),直線
時(shí),直線![]() 是否恒過定點(diǎn)?若是,求出定點(diǎn)坐標(biāo);若不是,請(qǐng)說明理由.
是否恒過定點(diǎn)?若是,求出定點(diǎn)坐標(biāo);若不是,請(qǐng)說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)拋物線的頂點(diǎn)為A,焦點(diǎn)為F.過F作直線l與拋物線交于點(diǎn)P、Q,直線AP、AQ分別與拋物線的準(zhǔn)線交于點(diǎn)M、N.問:直線l滿足什么條件時(shí),三直線PN、QM、AF恒交于一點(diǎn)?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某品牌經(jīng)銷商在一廣場(chǎng)隨機(jī)采訪男性和女性用戶各50名,其中每天玩微信超過6小時(shí)的用戶列為“微信控”,否則稱其為“非微信控”,調(diào)查結(jié)果如下:
微信控 | 非微信控 | 合計(jì) | |
男性 | 26 | 24 | 50 |
女性 | 30 | 20 | 50 |
合計(jì) | 56 | 44 | 100 |
(1)根據(jù)以上數(shù)據(jù),能否有95%的把握認(rèn)為“微信控”與“性別”有關(guān)?
(2)現(xiàn)從調(diào)查的女性用戶中按分層抽樣的方法選出5人,再隨機(jī)抽取3人贈(zèng)送禮品,記這3人中“微信控”的人數(shù)為![]() ,試求
,試求![]() 的分布列和數(shù)學(xué)期望.
的分布列和數(shù)學(xué)期望.
參考公式:  ,其中
,其中![]() .
.
參考數(shù)據(jù):
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】2019年春節(jié)期間,某超市準(zhǔn)備舉辦一次有獎(jiǎng)促銷活動(dòng),若顧客一次消費(fèi)達(dá)到400元?jiǎng)t可參加一次抽獎(jiǎng)活動(dòng),超市設(shè)計(jì)了兩種抽獎(jiǎng)方案.
方案一:一個(gè)不透明的盒子中裝有30個(gè)質(zhì)地均勻且大小相同的小球,其中10個(gè)紅球,20個(gè)白球,攪拌均勻后,顧客從中隨機(jī)抽取一個(gè)球,若抽到紅球則顧客獲得60元的返金券,若抽到白球則獲得20元的返金券,且顧客有放回地抽取3次.
方案二:一個(gè)不透明的盒子中裝有30個(gè)質(zhì)地均勻且大小相同的小球,其中10個(gè)紅球,20個(gè)白球,攪拌均勻后,顧客從中隨機(jī)抽取一個(gè)球,若抽到紅球則顧客獲得80元的返金券,若抽到白球則未中獎(jiǎng),且顧客有放回地抽取3次.
(1)現(xiàn)有兩位顧客均獲得抽獎(jiǎng)機(jī)會(huì),且都按方案一抽獎(jiǎng),試求這兩位顧客均獲得180元返金券的概率;
(2)若某顧客獲得抽獎(jiǎng)機(jī)會(huì).
①試分別計(jì)算他選擇兩種抽獎(jiǎng)方案最終獲得返金券的數(shù)學(xué)期望;
②為了吸引顧客消費(fèi),讓顧客獲得更多金額的返金券,該超市應(yīng)選擇哪一種抽獎(jiǎng)方案進(jìn)行促銷活動(dòng)?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在三棱柱![]() 中,點(diǎn)
中,點(diǎn)![]() 在平面
在平面![]() 內(nèi)運(yùn)動(dòng),使得二面角
內(nèi)運(yùn)動(dòng),使得二面角![]() 的平面角與二面角
的平面角與二面角![]() 的平面角互余,則點(diǎn)
的平面角互余,則點(diǎn)![]() 的軌跡是( )
的軌跡是( )

A. 一段圓弧 B. 橢圓的一部分 C. 拋物線 D. 雙曲線的一支
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】下列命題正確的是( )
A.已知隨機(jī)變量![]() ,若
,若![]() .則
.則![]()
B.已知分類變量![]() 與
與![]() 的隨機(jī)變量
的隨機(jī)變量![]() 的觀察值為
的觀察值為![]() ,則當(dāng)
,則當(dāng)![]() 的值越大時(shí),“
的值越大時(shí),“![]() 與
與![]() 有關(guān)”的可信度越小.
有關(guān)”的可信度越小.
C.在線性回歸模型中,計(jì)算其相關(guān)指數(shù)![]() ,則可以理解為:解析變量對(duì)預(yù)報(bào)變量的貢獻(xiàn)率約為
,則可以理解為:解析變量對(duì)預(yù)報(bào)變量的貢獻(xiàn)率約為![]()
D.若對(duì)于變量![]() 與
與![]() 的
的![]() 組統(tǒng)計(jì)數(shù)據(jù)的線性回歸模型中,相關(guān)指數(shù)
組統(tǒng)計(jì)數(shù)據(jù)的線性回歸模型中,相關(guān)指數(shù)![]() .又知?dú)埐钇椒胶蜑?/span>
.又知?dú)埐钇椒胶蜑?/span>![]() .那么
.那么![]() .(注意:
.(注意: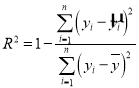 )
)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】“斗拱”是中國(guó)古代建筑中特有的構(gòu)件,從最初的承重作用,到明清時(shí)期集承重與裝飾作用于一體。在立柱頂、額枋和檐檁間或構(gòu)架間,從枋上加的一層層探出成弓形的承重結(jié)構(gòu)叫拱,拱與拱之間墊的方形木塊叫斗。如圖所示,是“散斗”(又名“三才升”)的三視圖,則它的體積為( )

A. ![]() B.
B. ![]() C. 53 D.
C. 53 D. ![]()
查看答案和解析>>