【題目】已知底面邊長為a的正三棱柱
（底面是等邊三角形的直三棱柱）的六個頂點在球
上，且球
與此正三棱柱的5個面都相切，則球與球的表面積之比為________.
口算小狀元口算速算天天練系列答案
天天練口算系列答案科目：高中數學 來源： 題型：
【題目】如圖1，在邊長為3的菱形
中，已知
，且
.將梯形
沿直線
折起，使
平面
，如圖2，
分別是
上的點.
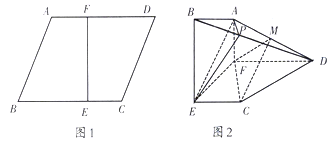
（1）若平面
平面
，求
的長；
（2）是否存在點
，使直線
與平面
所成的角是
？若存在，求出
的值；若不存在，請說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設橢圓
的右焦點為
，過點作與
軸垂直的直線
交橢圓于
，
兩點（點在第一象限），過橢圓的左頂點和上頂點的直線
與直線交于
點，且滿足
，設
為坐標原點，若
，
，則該橢圓的離心率為（ ）
A. 
B. 
C. 或 D. 
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在底面是正方形的四棱錐
中，
平面
，
，
是
的中點.
（1）求證：
平面
；
（2）在線段
上是否存在點
，使得
平面？若存在，求出
的值；若不存在，說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓
的離心率為
，左、右焦點分別為
、
，
為橢圓C上一點，且
的中點B在y軸上，
.
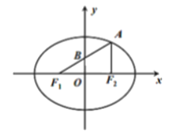
（1）求橢圓C的標準方程：
（2）若直線
交橢圓于P、Q兩點，若PQ的中點為N，O為原點，直線ON交直線
于點M，求
的最大值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】記數列
的前n項和為
，其中所有奇數項之和為
，所有偶數項之和為
若是等差數列，項數n為偶數，首項
，公差
，且
，求；
若數列的首項，滿足
，其中實常數
，且
，請寫出滿足上述條件常數t的兩個不同的值和它們所對應的數列．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】[選修4—4：坐標系與參數方程]
在直角坐標系
中，曲線
的方程為
．以坐標原點為極點，
軸正半軸為極軸建立極坐標系，曲線
的極坐標方程為
．
（1）求的直角坐標方程；
（2）若與有且僅有三個公共點，求的方程．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】秦九韶是我國南宋時期的數學家，普州（現四川省安岳縣）人，他在所著的《數書九章》中提出的多項式求值的秦九韶算法，至今仍是比較先進的算法．如圖所示的程序框圖給出了利用秦九韶算法求某多項式值的一個實例．若輸入n，x的值分別為5，2，則輸出v的值為( )
A. 64 B. 68
C. 72 D. 133
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
