
【題目】已知拋物線![]() 的頂點在原點,對稱軸為坐標(biāo)軸,它與雙曲線
的頂點在原點,對稱軸為坐標(biāo)軸,它與雙曲線![]() :
:![]() 交于點
交于點![]() ,拋物線
,拋物線![]() 的準(zhǔn)線過雙曲線
的準(zhǔn)線過雙曲線![]() 的左焦點.
的左焦點.
(1)求拋物線![]() 與雙曲線
與雙曲線![]() 的標(biāo)準(zhǔn)方程;
的標(biāo)準(zhǔn)方程;
(2)若斜率為![]() 的直線
的直線![]() 過點
過點![]() 且與拋物線只有一個公共點,求直線
且與拋物線只有一個公共點,求直線![]() 的方程.
的方程.
【答案】(1)拋物線方程為![]() ;雙曲線的方程為
;雙曲線的方程為![]() .(2)直線
.(2)直線![]() 的方程為
的方程為![]() 或
或![]()
【解析】
(1)根據(jù)拋物線![]() 的準(zhǔn)線過雙曲線
的準(zhǔn)線過雙曲線![]() 的左焦點,可知拋物線開口向右,則設(shè)拋物線方程為
的左焦點,可知拋物線開口向右,則設(shè)拋物線方程為![]() ,代入
,代入![]() 即可求得拋物線方程;由拋物線方程可得拋物線的準(zhǔn)線方程,進而得雙曲線的
即可求得拋物線方程;由拋物線方程可得拋物線的準(zhǔn)線方程,進而得雙曲線的![]() ,由雙曲線中
,由雙曲線中![]() 的關(guān)系及代入
的關(guān)系及代入![]() ,解方程可求得
,解方程可求得![]() ,即可得雙曲線的標(biāo)準(zhǔn)方程.
,即可得雙曲線的標(biāo)準(zhǔn)方程.
(2)討論直線![]() 的斜率
的斜率![]() 和
和![]() 兩種情況:當(dāng)
兩種情況:當(dāng)![]() 時一定成立,由所過定點坐標(biāo)可得直線方程;當(dāng)
時一定成立,由所過定點坐標(biāo)可得直線方程;當(dāng)![]() 時,聯(lián)立直線與拋物線方程,由判別式
時,聯(lián)立直線與拋物線方程,由判別式![]() 即可求得斜率
即可求得斜率![]() ,再由點斜式可得直線方程.
,再由點斜式可得直線方程.
(1)因為拋物線![]() 的準(zhǔn)線過雙曲線
的準(zhǔn)線過雙曲線![]() 的左焦點,
的左焦點,
設(shè)拋物線方程為![]()
由拋物線過![]() ,代入可得
,代入可得![]()
解得![]() ,所以拋物線方程為
,所以拋物線方程為![]()
拋物線的準(zhǔn)線方程為![]() ,所以雙曲線的
,所以雙曲線的![]()
同時將![]() 代入雙曲線方程,即
代入雙曲線方程,即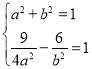 解方程組可得
解方程組可得![]()
所以雙曲線的標(biāo)準(zhǔn)方程為![]()
(2)斜率為![]() 的直線
的直線![]() 過點
過點![]() 且與拋物線只有一個公共點
且與拋物線只有一個公共點
當(dāng)![]() 時,直線方程為
時,直線方程為![]() ,滿足題意
,滿足題意
當(dāng)![]() 時,直線
時,直線![]() 可設(shè)為
可設(shè)為![]()
則![]() ,化簡可得
,化簡可得![]()
由與直線![]() 拋物線只有一個公共點
拋物線只有一個公共點
可得![]()
解得![]() ,所以直線
,所以直線![]() 的方程為
的方程為![]()
綜上可得直線![]() 的方程為
的方程為![]() 或
或![]()


科目:高中數(shù)學(xué) 來源: 題型:
【題目】某公司在招聘員工時,要進行筆試,面試和實習(xí)三個過程.筆試設(shè)置了3個題,每一個題答對得5分,否則得0分.面試則要求應(yīng)聘者回答3個問題,每一個問題答對得5分,否則得0分.并且規(guī)定在筆試中至少得到10分,才有資格參加面試,而筆試和面試得分之和至少為25分,才有實習(xí)的機會.現(xiàn)有甲去該公司應(yīng)聘,假設(shè)甲答對筆試中的每一個題的概率為![]() ,答對面試中的每一個問題的概率為
,答對面試中的每一個問題的概率為![]() .
.
(1)求甲獲得實習(xí)機會的概率;
(2)設(shè)甲在去應(yīng)聘過程中的所得分數(shù)為隨機變量![]() ,求
,求![]() 的分布列和數(shù)學(xué)期望.
的分布列和數(shù)學(xué)期望.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】為了解今年某校高三畢業(yè)班準(zhǔn)備報考飛行員學(xué)生的體重情況,將所得的數(shù)據(jù)整理后,畫出了頻率分布直方圖(如圖),已知圖中從左到右的前3個小組的頻率之比為1:2:3,其中第2小組的頻數(shù)為12.
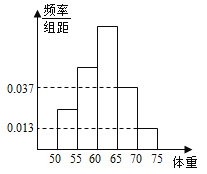
(1)求該校報考飛行員的總?cè)藬?shù);
(2)以這所學(xué)校的樣本數(shù)據(jù)來估計全省的總體數(shù)據(jù),若從全省報考飛行員的同學(xué)中(人數(shù)很多)任選三人,設(shè)![]() 表示體重超過60公斤的學(xué)生人數(shù),求
表示體重超過60公斤的學(xué)生人數(shù),求![]() 的分布列和數(shù)學(xué)期望.
的分布列和數(shù)學(xué)期望.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知圓C:x2+y2+2x﹣2y+1=0和拋物線E:y2=2px(p>0),圓C與拋物線E的準(zhǔn)線交于M、N兩點,△MNF的面積為p,其中F是E的焦點.
(1)求拋物線E的方程;
(2)不過原點O的動直線l交該拋物線于A,B兩點,且滿足OA⊥OB,設(shè)點Q為圓C上任意一動點,求當(dāng)動點Q到直線l的距離最大時直線l的方程.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() 的中心在坐標(biāo)原點,焦點在
的中心在坐標(biāo)原點,焦點在![]() 軸上,離心率為
軸上,離心率為![]() ,橢圓
,橢圓![]() 上的點到焦點距離的最大值為
上的點到焦點距離的最大值為![]() .
.
(Ⅰ)求橢圓![]() 的標(biāo)準(zhǔn)方程;
的標(biāo)準(zhǔn)方程;
(Ⅱ)若過點![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 交于不同的兩點
交于不同的兩點![]() ,且
,且![]() ,求實數(shù)
,求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】甲與乙午覺醒來后,發(fā)現(xiàn)自己的手表因故停止轉(zhuǎn)動,于是他們想借助收音機,利用電臺整點報時確認時間.
(1)求甲等待的時間不多于10分鐘的概率;
(2)求甲比乙多等待10分鐘以上的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知圓C經(jīng)過![]() 、
、![]() 兩點,且圓心在直線
兩點,且圓心在直線![]() 上.
上.
(1)求圓C的方程;
(2)若直線![]() 經(jīng)過點
經(jīng)過點![]() 且與圓C相切,求直線
且與圓C相切,求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某中學(xué)數(shù)學(xué)老師分別用兩種不同教學(xué)方式對入學(xué)數(shù)學(xué)平均分和優(yōu)秀率都相同的甲、乙兩個高一新班(人數(shù)均為![]() 人)進行教學(xué)(兩班的學(xué)生學(xué)習(xí)數(shù)學(xué)勤奮程度和自覺性一致),數(shù)學(xué)期終考試成績莖葉圖如下:
人)進行教學(xué)(兩班的學(xué)生學(xué)習(xí)數(shù)學(xué)勤奮程度和自覺性一致),數(shù)學(xué)期終考試成績莖葉圖如下:
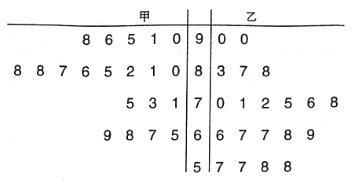
(1)現(xiàn)從乙班數(shù)學(xué)成績不低于![]() 分的同學(xué)中隨機抽取兩名同學(xué),求至少有一名成績?yōu)?/span>
分的同學(xué)中隨機抽取兩名同學(xué),求至少有一名成績?yōu)?/span>![]() 分的同學(xué)被抽中的概率;
分的同學(xué)被抽中的概率;
(2)學(xué)校規(guī)定:成績不低于![]() 分的優(yōu)秀,請?zhí)顚懴旅娴?/span>
分的優(yōu)秀,請?zhí)顚懴旅娴?/span>![]() 聯(lián)表,并判斷有多大把握認為“成績優(yōu)秀與教學(xué)方式有關(guān)”.
聯(lián)表,并判斷有多大把握認為“成績優(yōu)秀與教學(xué)方式有關(guān)”.
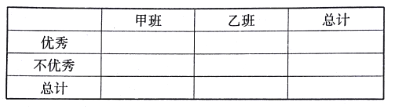
附:參考公式及數(shù)據(jù)

查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在四棱錐O﹣ABCD中,OA⊥底面ABCD,且底面ABCD是邊長為2的正方形,且OA=2,M,N分別為OA,BC的中點.
(1)求證:直線MN![]() 平面OCD;
平面OCD;
(2)求點B到平面DMN的距離.

查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com