
【題目】已知函數![]() ,其中實數
,其中實數![]() 為常數,
為常數,![]() 為自然對數的底數.
為自然對數的底數.
(1)當![]() 時,求函數
時,求函數![]() 的單調區間;
的單調區間;
(2)當![]() 時,解關于
時,解關于![]() 的不等式
的不等式![]() ;
;
(3)當![]() 時,如果函數
時,如果函數![]() 不存在極值點,求
不存在極值點,求![]() 的取值范圍.
的取值范圍.
【答案】(1)單調遞增區間為![]() ;單調遞減區間為
;單調遞減區間為![]() .(2)
.(2)![]() (3)
(3)![]()
【解析】試題分析:把![]() 代入由于對數的真數為正數,函數定義域為
代入由于對數的真數為正數,函數定義域為![]() ,所以函數化為
,所以函數化為![]() ,求導后在定義域下研究函數的單調性給出單調區間;代入
,求導后在定義域下研究函數的單調性給出單調區間;代入![]() ,
,![]() ,分
,分![]() 和
和![]() 兩種情況解不等式;當
兩種情況解不等式;當![]() 時,
時,![]() ,求導
,求導![]() ,函數
,函數![]() 不存在極值點,只需
不存在極值點,只需![]() 恒成立,根據這個要求得出
恒成立,根據這個要求得出![]() 的范圍.
的范圍.
試題解析:
(1)![]() 時,
時,![]() ,
,
令![]() ,解得
,解得![]() ,
,
且![]() 時,
時,![]() ,
,![]() 單調遞減;
單調遞減;
![]() 時,
時,![]() ,
,![]() 單調遞增.
單調遞增.
所以![]() 單調遞增區間為
單調遞增區間為![]() ;單調遞減區間為
;單調遞減區間為![]() .
.
(2)![]() 時,
時,![]() .
.
當![]() 時,原不等式可化為
時,原不等式可化為![]() .
.
記![]() ,則
,則![]() ,
,
當![]() 時,
時,![]() ,
,
所以![]() 在
在![]() 單調遞增,又
單調遞增,又![]() ,故不等式解為
,故不等式解為![]() ;
;
當![]() 時,原不等式可化為
時,原不等式可化為![]() ,顯然不成立,
,顯然不成立,
綜上,原不等式的解集為![]() .
.
(3)![]() 時,
時,![]() ,
,
![]() ,記
,記![]() ,
,
因為![]() 時,
時,![]() ,
,
所以![]() 不存在極值點時
不存在極值點時![]() 恒成立.
恒成立.
由![]() ,解得
,解得![]()
且![]() 時,
時,![]() ,
,![]() 單調遞減;
單調遞減;
![]() 時,
時,![]() ,
,![]() 單調遞增.
單調遞增.
所以![]() ,解得
,解得![]() .
.


科目:高中數學 來源: 題型:
【題目】頂點在原點,焦點在x軸正半軸的拋物線,經過點(3,6),
(1)求拋物線截直線y=2x﹣6所得的弦長.
(2)討論直線y=kx+1與拋物線的位置關系,并求出相應的k的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,將一矩形花壇ABCD擴建成一個更大的矩形花壇AMPN,要求B點在AM上,D點在AN上,且對角線MN過點C,已知AB=3米,AD=2米.
(Ⅰ)要使矩形AMPN的面積大于32平方米,則DN的長應在什么范圍內?
(Ⅱ)當DN的長度為多少時,矩形花壇AMPN的面積最小?并求出最小值.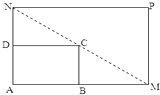
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】給出下列命題:
①直線l的方向向量為 ![]() =(1,﹣1,2),直線m的方向向量
=(1,﹣1,2),直線m的方向向量 ![]() =(2,1,﹣
=(2,1,﹣ ![]() ),則l與m垂直;
),則l與m垂直;
②直線l的方向向量 ![]() =(0,1,﹣1),平面α的法向量
=(0,1,﹣1),平面α的法向量 ![]() =(1,﹣1,﹣1),則l⊥α;
=(1,﹣1,﹣1),則l⊥α;
③平面α、β的法向量分別為 ![]() =(0,1,3),
=(0,1,3), ![]() =(1,0,2),則α∥β;
=(1,0,2),則α∥β;
④平面α經過三點A(1,0,﹣1),B(0,1,0),C(﹣1,2,0),向量 ![]() =(1,u,t)是平面α的法向量,則u+t=1.
=(1,u,t)是平面α的法向量,則u+t=1.
其中真命題的是 . (把你認為正確命題的序號都填上)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知集合A={x|x2﹣5x﹣6<0},集合B={x|6x2﹣5x+1≥0},集合 ![]()
(1)求A∩B;
(2)若A∪C=C,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某人有樓房一幢,室內面積共計180m2 , 擬分割成兩類房間作為旅游客房,大房間每間面積為18m2 , 可住游客5名,每名游客每天住宿費40元;小房間每間面積為15m2 , 可以住游客3名,每名游客每天住宿費50元;裝修大房間每間需要1000元,裝修小房間每間需要600元.如果他只能籌款8000元用于裝修,且假定游客能住滿客房,他應隔出大房間和小房間各多少間,才能獲得最大收益? 
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com