
【題目】已知等比數列![]() 的前
的前![]() 項和為
項和為![]() ,公比
,公比![]() ,
, ![]() ,
, ![]() .
.
(Ⅰ)求數列{an}的通項公式;
(Ⅱ)設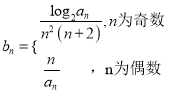 ,
, ![]() 為{
為{![]() }的前
}的前![]() 項和,求
項和,求![]() .
.
【答案】(Ⅰ) ![]() ;(Ⅱ)
;(Ⅱ) ![]() .
.
【解析】試題分析:
(Ⅰ)由題意求得數列的首項、公比均為2,則數列的通項公式為an=2n;
(Ⅱ)由題意裂項求和可得![]() .
.
試題解析:
(I)∵等比數列{an}的前n項和為Sn,公比q>0,S2=2a2﹣2,S3=a4﹣2.
∴a3=a4﹣2a2,可得a2q=a2(q2﹣2),
∴q2﹣q﹣2=0,解得q=2.∴a1+a2=2a2﹣2,即a1=a2﹣2=2a1﹣2,解得a1=2.
∴an=2n.
(II)n為奇數時,bn=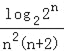 =
=![]() =
=![]() .
.
n為偶數時,bn=![]() .
.
∴T2n=![]()
![]() +
+![]() +…+
+…+![]() +
+![]() +…+
+…+![]()
=![]() +
+![]() +…+
+…+![]()
=![]() +
+![]() +…+
+…+![]() .
.
設A=![]() +…+
+…+![]() ,
,
則![]() A=
A=![]() +…+
+…+![]() +
+![]() ,
,
∴![]() A=
A=![]() +…+
+…+![]() ﹣
﹣![]() =
=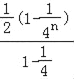 ﹣
﹣![]() ,
,
∴A=![]() ﹣
﹣![]() .
.
∴T2n=![]() +
+![]() ﹣
﹣![]() .
.


 考前必練系列答案
考前必練系列答案科目:高中數學 來源: 題型:
【題目】己知函數f(x)=loga(x+1),g(x)=2loga(2x+t)(t∈R),a>0,且a≠1.
(1)若1是關于x的方程f(x)﹣g(x)=0的一個解,求t的值;
(2)當0<a<1且t=﹣1時,解不等式f(x)≤g(x);
(3)若函數F(x)=af(x)+tx2﹣2t+1在區間(﹣1,2]上有零點,求t的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設復數z=a+i(i是虛數單位,a∈R,a>0),且|z|=![]() .
.
(Ⅰ)求復數z;
(Ⅱ)在復平面內,若復數![]() +
+![]() (m∈R)對應的點在第四象限,求實數m取值范圍.
(m∈R)對應的點在第四象限,求實數m取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列各組函數,在同一直角坐標系中f(x)與g(x)相同的一組是( )
A.f(x)= ![]() ,g(x)=
,g(x)= ![]()
B.f(x)= ![]() ,g(x)=x﹣3
,g(x)=x﹣3
C.f(x)= ![]() ,g(x)=
,g(x)= ![]()
D.f(x)=x,g(x)=lg(10x)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】徐州、蘇州兩地相距500千米,一輛貨車從徐州勻速行駛到蘇州,規定速度不得超過100千米/小時.已知貨車每小時的運輸成本(以元為單位)由可變部分和固定部分組成:可變部分與速度v(千米/時)的平方成正比,比例系數為0.01;固定部分為a元(a>0).
(1)把全程運輸成本y(元)表示為速度v(千米/時)的函數,并指出這個函數的定義域;
(2)為了使全程運輸成本最小,汽車應以多大速度行駛?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com