
【題目】已知函數![]() ,
,![]() .
.
(1)證明:![]() ,直線
,直線![]() 都不是曲線
都不是曲線![]() 的切線;
的切線;
(2)若![]() ,使
,使![]() 成立,求實數
成立,求實數![]() 的取值范圍.
的取值范圍.
【答案】(Ⅰ)見解析; (Ⅱ)![]() .
.
【解析】
試題(1)若直線![]() 與曲線
與曲線![]() 相切,因直線
相切,因直線![]() 過定點
過定點![]() ,若設切點
,若設切點![]() 則可得
則可得![]() ①,又
①,又![]() ,
,![]() 上單調遞增,當且僅當
上單調遞增,當且僅當![]() 時,①成立,這與
時,①成立,這與![]() 矛盾,結論得證.
矛盾,結論得證.
(2)![]() 可轉化為
可轉化為![]() ,令
,令![]() ,
,![]() ,
,![]() ,分類討論求
,分類討論求![]() 的最小值即可.
的最小值即可.
試題解析: (1)![]() 的定義域為
的定義域為![]() ,
,![]() ,直線
,直線![]() 過定點
過定點![]() ,若直線
,若直線![]() 與曲線
與曲線![]() 相切于點
相切于點![]() (
(![]() 且
且![]() ),則
),則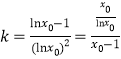 ,即
,即![]() ①,設
①,設![]() ,
,![]() ,則
,則![]() ,所以
,所以![]() 在
在![]() 上單調遞增,又
上單調遞增,又![]() ,從而當且僅當
,從而當且僅當![]() 時,①成立,這與
時,①成立,這與![]() 矛盾.
矛盾.
所以,![]() ,直線
,直線![]() 都不是曲線
都不是曲線![]() 的切線;
的切線;
(2)![]() 即
即![]() ,令
,令![]() ,
,![]() ,
,
則![]() ,使
,使![]() 成立
成立![]() ,
,
![]() .
.
(i)當![]() 時,
時,![]() ,
,![]() 在
在![]() 上為減函數,于是
上為減函數,于是![]() ,由
,由![]() 得
得![]() ,滿足
,滿足![]() ,所以
,所以![]() 符合題意;
符合題意;
(ii)當![]() 時,由
時,由![]() 及
及![]() 的單調性知
的單調性知![]() 在
在![]() 上為增函數,所以
上為增函數,所以![]() ,即
,即![]() .
.
①若![]() ,即
,即![]() ,則
,則![]() ,所以
,所以![]() 在
在![]() 為增函數,于是
為增函數,于是![]() ,不合題意;
,不合題意;
②若![]() ,即
,即![]() ,則由
,則由![]() ,
,![]() 及
及![]() 的單調性知存在唯一
的單調性知存在唯一![]() ,使
,使![]() ,且當
,且當![]() 時,
時,![]() ,
,![]() 為減函數;當
為減函數;當![]() 時,
時,![]() ,
,![]() 為增函數;
為增函數;
所以![]() ,由
,由![]() 得
得![]() ,這與
,這與![]() 矛盾,不合題意.
矛盾,不合題意.
綜上可知,![]() 的取值范圍是
的取值范圍是![]() .
.


科目:高中數學 來源: 題型:
【題目】有![]() 名乒乓球選手進行單循環賽(無和局),比賽結果顯示:任意5人中既有1人勝于其余4人,又有1人負于其余4人.則恰勝兩場的人數為______個.
名乒乓球選手進行單循環賽(無和局),比賽結果顯示:任意5人中既有1人勝于其余4人,又有1人負于其余4人.則恰勝兩場的人數為______個.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某班在一次個人投籃比賽中,記錄了在規定時間內投進![]() 個球的人數分布情況:
個球的人數分布情況:
進球數 | 0 | 1 | 2 | 3 | 4 | 5 |
投進 | 1 | 2 | 7 | 2 |
其中![]() 和
和![]() 對應的數據不小心丟失了,已知進球3個或3個以上,人均投進4個球;進球5個或5個以下,人均投進2.5個球.
對應的數據不小心丟失了,已知進球3個或3個以上,人均投進4個球;進球5個或5個以下,人均投進2.5個球.
(1)投進3個球和4個球的分別有多少人?
(2)從進球數為3,4,5的所有人中任取2人,求這2人進球數之和為8的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
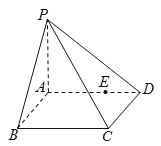
【題目】如圖,四棱錐![]() 中,
中,![]() 是矩形,
是矩形,![]() 平面
平面![]() ,
,![]() ,
,![]() ,四棱錐外接球的球心為
,四棱錐外接球的球心為![]() ,點
,點![]() 是棱
是棱![]() 上的一個動點.給出如下命題:①直線
上的一個動點.給出如下命題:①直線![]() 與直線
與直線![]() 是異面直線;②
是異面直線;②![]() 與
與![]() 一定不垂直;③三棱錐
一定不垂直;③三棱錐![]() 的體積為定值;④
的體積為定值;④![]() 的最小值為
的最小值為![]() .其中正確命題的序號是______________.(將你認為正確的命題序號都填上)
.其中正確命題的序號是______________.(將你認為正確的命題序號都填上)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某學校開展主題為“垃圾分類,綠色生活新時尚”的宣傳活動,為了解學生對垃圾分類知識的掌握情況,該校環保社團成員在校園內隨機抽取了部分學生進行問卷調查,將他們的得分按優秀、良好、合格、待合格四個等級進行統計,并繪制了如下不完整的統計表和條形統計圖.請根據以下信息,解答下列問題:
等級 | 頻數 | 頻率 |
優秀 | 21 | 42% |
良好 |
| 40% |
合格 | 6 |
|
待合格 | 3 | 6% |
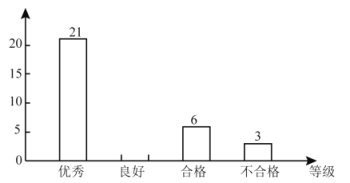
(1)本次調查隨機抽取了__________名學生,表中![]() __________,
__________,![]() __________;
__________;
(2)補全條形統計圖;
(3)若全校有![]() 名學生,請你估計該校掌握垃圾分類知識達到“優秀”和“良好”等級的學生共有多少人.
名學生,請你估計該校掌握垃圾分類知識達到“優秀”和“良好”等級的學生共有多少人.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列4個命題:
(1)有兩個面互相平行,其余四個面都是全等的等腰梯形的六面體是正四棱臺;
(2)底面是正三角形,其余各面都是等腰三角形的棱錐是正三棱錐;
(3)各側面都是等腰三角形的四棱錐是正四棱錐;
(4)底面是正三角形,相鄰兩側而所成的二面角都相等的三棱錐是正三棱錐
中,假命題的個數為( ).
A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com