
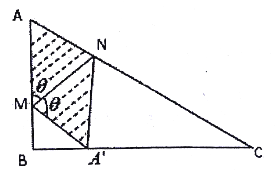
【題目】如圖,某小區準備將閑置的一直角三角形地塊開發成公共綠地,圖中![]() .設計時要求綠地部分(如圖中陰影部分所示)有公共綠地走道
.設計時要求綠地部分(如圖中陰影部分所示)有公共綠地走道![]() ,且兩邊是兩個關于走道
,且兩邊是兩個關于走道![]() 對稱的三角形(
對稱的三角形(![]() 和
和![]() ).現考慮方便和綠地最大化原則,要求點
).現考慮方便和綠地最大化原則,要求點![]() 與點
與點![]() 均不重合,
均不重合,![]() 落在邊
落在邊![]() 上且不與端點
上且不與端點![]() 重合,設
重合,設![]() .
.
(1)若![]() ,求此時公共綠地的面積;
,求此時公共綠地的面積;
(2)為方便小區居民的行走,設計時要求![]() 的長度最短,求此時綠地公共走道
的長度最短,求此時綠地公共走道![]() 的長度.
的長度.
 高中必刷題系列答案
高中必刷題系列答案科目:高中數學 來源: 題型:
【題目】設D是函數y=f(x)定義域內的一個區間,若存在x0∈D,使f(x0)=﹣x0 , 則稱x0是f(x)的一個“次不動點”,也稱f(x)在區間D上存在次不動點.若函數f(x)=ax2﹣3x﹣a+ ![]() 在區間[1,4]上存在次不動點,則實數a的取值范圍是( )
在區間[1,4]上存在次不動點,則實數a的取值范圍是( )
A.(﹣∞,0)
B.(0, ![]() )
)
C.[ ![]() ,+∞)
,+∞)
D.(﹣∞, ![]() ]
]
查看答案和解析>>
科目:高中數學 來源: 題型:
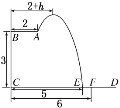
【題目】某跳水運動員在一次跳水訓練時的跳水曲線為如圖所示拋物線的一段.已知跳水板![]() 長為
長為![]() ,跳水板距水面
,跳水板距水面![]() 的高
的高![]() 為
為![]() .為安全和空中姿態優美,訓練時跳水曲線應在離起跳點
.為安全和空中姿態優美,訓練時跳水曲線應在離起跳點![]() 處水平距
處水平距![]()
![]() 時達到距水面最大高度
時達到距水面最大高度![]() ,規定:以
,規定:以![]() 為橫軸,
為橫軸,![]() 為縱軸建立直角坐標系.
為縱軸建立直角坐標系.
(1)當![]() 時,求跳水曲線所在的拋物線方程;
時,求跳水曲線所在的拋物線方程;
(2)若跳水運動員在區域![]() 內入水時才能達到比較好的訓練效果,求此時
內入水時才能達到比較好的訓練效果,求此時![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在正方體ABCD﹣A1B1C1D1中,E,F分別是棱A1B1 , B1C1的中點,O是AC與BD的交點,面OEF與面BCC1B1相交于m,面OD1E與面BCC1B1相交于n,則直線m,n的夾角為( )
A.0
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{an}滿足an= ![]() ,若從{an}中提取一個公比為q的等比數列{
,若從{an}中提取一個公比為q的等比數列{ ![]() },其中k1=1,且k1<k2<…<kn , kn∈N* , 則滿足條件的最小q的值為 .
},其中k1=1,且k1<k2<…<kn , kn∈N* , 則滿足條件的最小q的值為 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】將函數y=sin(x+ ![]() )的圖象上各點的橫坐標壓縮為原來的
)的圖象上各點的橫坐標壓縮為原來的 ![]() 倍(縱坐標不變),所得函數在下面哪個區間單調遞增( )
倍(縱坐標不變),所得函數在下面哪個區間單調遞增( )
A.(﹣ ![]() ,
, ![]() )
)
B.(﹣ ![]() ,
, ![]() )
)
C.(﹣ ![]() ,
, ![]() )
)
D.(﹣ ![]() ,
, ![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】給出下列說法:
①集合![]() 與集合
與集合![]() 是相等集合;
是相等集合;
②不存在實數![]() ,使
,使![]() 為奇函數;
為奇函數;
③若![]() ,且f(1)=2,則
,且f(1)=2,則![]() ;
;
④對于函數![]()
![]() 在同一直角坐標系中,若
在同一直角坐標系中,若![]() ,則函數
,則函數![]() 的圖象關于直線
的圖象關于直線![]() 對稱;
對稱;
⑤對于函數![]()
![]() 在同一直角坐標系中,函數
在同一直角坐標系中,函數![]() 與
與![]() 的圖象關于直線
的圖象關于直線![]() 對稱;其中正確說法是____________.
對稱;其中正確說法是____________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓心在坐標原點的圓O經過圓![]() 與圓
與圓![]() 的交點,A、B是圓O與y軸的交點,P為直線y=4上的動點,PA、PB與圓O的另一個交點分別為M、N.
的交點,A、B是圓O與y軸的交點,P為直線y=4上的動點,PA、PB與圓O的另一個交點分別為M、N.
(1)求圓O的方程;
(2)求證:直線MN過定點.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com