
【題目】已知![]() ,
, ![]() 是
是![]() 的導函數.
的導函數.
(1)求![]() 的極值;
的極值;
(2)證明:對任意實數![]() ,都有
,都有![]() 恒成立;
恒成立;
(3)若![]() 在
在![]() 時恒成立,求實數
時恒成立,求實數![]() 的取值范圍.
的取值范圍.
【答案】(Ⅰ)見解析(Ⅱ)見解析(Ⅲ)![]() .
.
【解析】試題分析:(Ⅰ)由題意得處![]() ,進而
,進而![]() ,分
,分![]() 和
和![]() 兩種情況討論,即可求解;
兩種情況討論,即可求解;
(Ⅱ)由![]() ,則要證
,則要證![]()
![]() ,只需證
,只需證![]() .
.
令![]() ,利用導數得出函數
,利用導數得出函數![]() 的性質,即可作出證明.
的性質,即可作出證明.
(Ⅲ)由(Ⅱ)知![]() 恒成立,可得
恒成立,可得![]() ,分
,分![]() 和
和![]() 兩種情況討論,即可求解實數
兩種情況討論,即可求解實數![]() 的值.
的值.
試題解析:
(Ⅰ)![]() ,
, ![]() ,
, ![]() ,
,
當![]() 時,
時, ![]() 恒成立,
恒成立, ![]() 無極值;
無極值;
當![]() 時,
時, ![]() ,即
,即![]() ,
,
由![]() ,得
,得![]() ;由
;由![]() ,得
,得![]() ,
,
所以當![]() 時,有極小值
時,有極小值![]() .
.
(Ⅱ)因為![]() ,所以,要證
,所以,要證![]()
![]() ,只需證
,只需證![]() .
.
令![]() ,則
,則![]() ,且
,且![]() ,得
,得![]() ;
; ![]() ,得
,得![]() ,
,
∴![]() 在
在![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增,
上單調遞增,
∴![]() ,即
,即![]() 恒成立,
恒成立,
∴對任意實數![]() ,都有
,都有![]()
![]() 恒成立.
恒成立.
(Ⅲ)令![]() ,則
,則![]() ,注意到
,注意到![]() ,
,
由(Ⅱ)知![]() 恒成立,故
恒成立,故![]() ,
,
①當![]() 時,
時, ![]() ,
, ![]() ,
,
于是當![]() 時,
時, ![]() ,即
,即![]() 成立.
成立.
②當![]() 時,由
時,由![]() (
(![]() )可得
)可得![]() (
(![]() ).
).
![]() ,
,
故當![]() 時,
時, ![]() ,
,
于是當![]() 時,
時, ![]() ,
, ![]() 不成立.
不成立.
綜上, ![]() 的取值范圍為
的取值范圍為![]() .
.


科目:高中數學 來源: 題型:
【題目】已知函數![]() ,
, ![]() (
(![]() 為自然對數的底數).
為自然對數的底數).
(1)設曲線![]() 在
在![]() 處的切線為
處的切線為![]() ,若
,若![]() 與點
與點![]() 的距離為
的距離為![]() ,求
,求![]() 的值;
的值;
(2)若對于任意實數![]() ,
, ![]() 恒成立,試確定
恒成立,試確定![]() 的取值范圍;
的取值范圍;
(3)當![]() 時,函數
時,函數![]() 在
在![]() 上是否存在極值?若存在,請求出極值;若不存在,請說明理由.
上是否存在極值?若存在,請求出極值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校計劃面向高一年級1240名學生開設校本選修課程,為確保工作的順利實施,按性別進行分層抽樣,現抽取124名學生對社會科學類、自然科學類這兩大類校本選修課程進行選課意向調查,其中男生有65人.在這124名學生中選修社會科學類的男生有22人、女生有40人.
(1)根據以上數據完成下列列聯表;
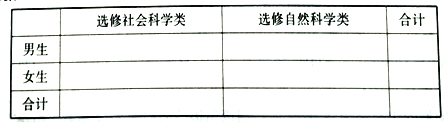
(2)判斷能否有99.9%的把握認為科類的選修與性別有關?
附: 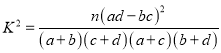 ,其中
,其中![]()
| 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系中,以原點為極點, ![]() 軸正半軸為極軸建立極坐標系,并在兩坐標系中取相同的長度單位.已知曲線
軸正半軸為極軸建立極坐標系,并在兩坐標系中取相同的長度單位.已知曲線![]() 的極坐標方程為
的極坐標方程為![]() ,直線
,直線![]() 的參數方程為
的參數方程為
![]() (
(![]() 為參數,
為參數, ![]() 為直線的傾斜角).
為直線的傾斜角).
(1)寫出直線![]() 的普通方程和曲線
的普通方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)若直線![]() 與曲線
與曲線![]() 有唯一的公共點,求角
有唯一的公共點,求角![]() 的大小.
的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】隨著智能手機的發展,微信越來越成為人們交流的一種方式,某機構對使用微信交流的態度進行調查,隨機調查了50人,他們年齡的頻數分布及對使用微信交流贊成人數如表:
年齡(歲) |
|
|
|
|
|
|
頻數 | 5 | 10 | 15 | 10 | 5 | 5 |
贊成人數 | 5 | 10 | 12 | 7 | 2 | 1 |
(1)由以上統計數據填寫下面![]() 列聯表,并判斷是否有99%的把握認為年齡45歲為分界點對使用微信交流的態度有差異;
列聯表,并判斷是否有99%的把握認為年齡45歲為分界點對使用微信交流的態度有差異;
年齡不低于45歲的人 | 年齡低于45歲的人 | 合計 | |
贊成 | |||
不贊成 | |||
合計 |
(2)若對年齡分別在![]() ,
, ![]() 的被調查人中各抽取一人進行追蹤調查,求選中的2人中至少有一人贊成使用微信交流的概率.
的被調查人中各抽取一人進行追蹤調查,求選中的2人中至少有一人贊成使用微信交流的概率.
參考公式: ![]() ,其中
,其中![]()
參考數據:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】給出下列命題:①定義在![]() 上的函數
上的函數![]() 滿足
滿足![]() ,則
,則![]() 一定不是
一定不是![]() 上的減函數;
上的減函數;
②用反證法證明命題“若實數![]() ,滿足
,滿足![]() ,則
,則![]() 都為0”時,“假設命題的結論不成立”的敘述是“假設
都為0”時,“假設命題的結論不成立”的敘述是“假設![]() 都不為0”;
都不為0”;
③把函數![]() 的圖象向右平移
的圖象向右平移![]() 個單位長度,所得到的圖象的函數解析式為
個單位長度,所得到的圖象的函數解析式為![]() ;
;
④“![]() ”是“函數
”是“函數![]() 為奇函數”的充分不必要條件.
為奇函數”的充分不必要條件.
其中所有正確命題的序號為__________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某中學為研究學生的身體素質與課外體育鍛煉時間的關系,對400名高一學生的一周課外體育鍛煉時間進行調查,結果如下表所示:現采用分層抽樣的方法抽取容量為20的樣本.
(1)其中課外體育鍛煉時間在![]() 分鐘內的學生應抽取多少人?
分鐘內的學生應抽取多少人?
(2)若從(1)中被抽取的學生中隨機抽取2名,求這2名學生課外體育鍛煉時間均在![]() 分鐘內的概率.
分鐘內的概率.
鍛煉時間(分鐘) |
|
|
|
|
|
|
人數 | 40 | 60 | 80 | 100 | 80 | 40 |
查看答案和解析>>
科目:高中數學 來源: 題型:
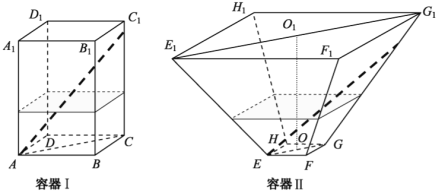
【題目】如圖,水平放置的正四棱柱形玻璃容器Ⅰ和正四棱臺形玻璃容器Ⅱ的高均為32cm,容器Ⅰ的底面對角線AC的長為10![]() cm,容器Ⅱ的兩底面對角線
cm,容器Ⅱ的兩底面對角線![]() ,
,![]() 的長分別為14cm和62cm.分別在容器Ⅰ和容器Ⅱ中注入水,水深均為12cm.現有一根玻璃棒l,其長度為40cm.(容器厚度、玻璃棒粗細均忽略不計)
的長分別為14cm和62cm.分別在容器Ⅰ和容器Ⅱ中注入水,水深均為12cm.現有一根玻璃棒l,其長度為40cm.(容器厚度、玻璃棒粗細均忽略不計)
(1)將![]() 放在容器Ⅰ中,
放在容器Ⅰ中,![]() 的一端置于點A處,另一端置于側棱
的一端置于點A處,另一端置于側棱![]() 上,求
上,求![]() 沒入水中部分的長度;
沒入水中部分的長度;
(2)將![]() 放在容器Ⅱ中,
放在容器Ⅱ中,![]() 的一端置于點E處,另一端置于側棱
的一端置于點E處,另一端置于側棱![]() 上,求
上,求![]() 沒入水中部分的長度.
沒入水中部分的長度.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“開門大吉”是某電視臺推出的游戲節目,選手面對1![]() 號8扇大門,依次按響門上的門鈴,門鈴會播放一段音樂(將一首經典流行歌曲以單音色旋律的方式演繹),選手需正確回答出這首歌的名字,方可獲得該扇門對應的家庭夢想基金,在一次場外調查中,發現參賽選手多數分為兩個年齡段:
號8扇大門,依次按響門上的門鈴,門鈴會播放一段音樂(將一首經典流行歌曲以單音色旋律的方式演繹),選手需正確回答出這首歌的名字,方可獲得該扇門對應的家庭夢想基金,在一次場外調查中,發現參賽選手多數分為兩個年齡段: ![]() ;
; ![]() (單位:歲),其猜對歌曲名稱與否的人數如圖所示.
(單位:歲),其猜對歌曲名稱與否的人數如圖所示.

(Ⅰ)寫出![]() 列聯表;判斷是否有
列聯表;判斷是否有![]() 的把握認為猜對歌曲名稱是否與年齡有關;說明你的理由;(如表的臨界值表供參考)
的把握認為猜對歌曲名稱是否與年齡有關;說明你的理由;(如表的臨界值表供參考)
| 0.10 | 0.05 | 0.010 | 0.005 |
| 2.706 | 3.841 | 6.635 | 7.879 |
(Ⅱ)現計劃在這次場外調查中按年齡段用分層抽樣的方法選取6名選手,并抽取3名幸運選手,求3名幸運選手中恰好有一人在![]() 歲之間的概率.
歲之間的概率.
(參考公式:  ,其中
,其中![]() )
)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com