
(本題滿分12分,第1小題6分,第2小題6分)
已知集合A={x| | x–a | < 2,xÎR },B={x| <1,xÎR }.
<1,xÎR }.
(1) 求A、B;
(2) 若 ,求實數a的取值范圍.
,求實數a的取值范圍.
(1)A={x| a–2<x<a+2};B={x|–2<x<3}.(2)0≤a≤1.
解析試題分析:(1) 由| x–a | < 2,得a–2<x<a+2,所以A={x| a–2<x<a+2}………………………3分
由 <1,得
<1,得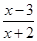 <0,即 –2<x<3,所以B={x|–2<x<3}.…………………………6分
<0,即 –2<x<3,所以B={x|–2<x<3}.…………………………6分
(2) 若AÍB,所以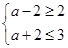 ,…………………………………………………………10分
,…………………………………………………………10分
所以0≤a≤1.………………………………………………………………………………12分
考點:含絕對值的不等式的解法;分式不等式的解法;集合間的關系。
點評:解分式不等式的主要步驟是:移項—通分—分式化整式。屬于基礎題型。


科目:高中數學 來源: 題型:解答題
(本題12分)已知集合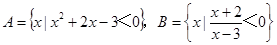
(Ⅰ)在區間(-4,4)上任取一個實數x,求“x∈A∩B”的概率;
(Ⅱ)設(a,b)為有序實數對,其中a是從集合A中任取的一個整數,b是從集合B中任取的一個整數,求“b-a∈A∪B”的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com