
【題目】如圖,在平面直角坐標系xOy中,已知拋物線的焦點F在y軸上,其準線與雙曲線![]()
![]() 的下準線重合.
的下準線重合.

(1)求拋物線的標準方程;
(2)設A(![]() ,
,![]() )(
)(![]() >0)是拋物線上一點,且AF=
>0)是拋物線上一點,且AF=![]() ,B是拋物線的準線與y軸的交點.過點A作拋物線的切線l,過點B作l的平行線l′,直線l′與拋物線交于點M,N,求△AMN的面積.
,B是拋物線的準線與y軸的交點.過點A作拋物線的切線l,過點B作l的平行線l′,直線l′與拋物線交于點M,N,求△AMN的面積.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)根據(jù)雙曲線的下準線求得拋物線的準線方程,由此求得拋物線的標準方程.
(2)根據(jù)拋物線的定義求得![]() 點的坐標,由此求得切線
點的坐標,由此求得切線![]() 的方程,求得
的方程,求得![]() 點的坐標,進而求得直線
點的坐標,進而求得直線![]() 的方程,由此求得弦長
的方程,由此求得弦長![]() ,利用點到直線距離公式求得
,利用點到直線距離公式求得![]() 到直線
到直線![]() 的距離,進而求得三角形
的距離,進而求得三角形![]() 的面積.
的面積.
(1)雙曲線![]() 的下準線方程為
的下準線方程為![]() .設拋物線的標準方程為
.設拋物線的標準方程為![]() ,由題意,
,由題意,![]() ,所以
,所以![]() ,所以拋物線的標準方程為
,所以拋物線的標準方程為![]() .
.
(2)由![]() ,得
,得![]() ,所以
,所以![]() .由
.由![]() 即
即![]() ,得
,得![]() ,所以拋物線在
,所以拋物線在![]() 點處的切線
點處的切線![]() 的斜率為
的斜率為![]() ,所以直線
,所以直線![]() 的方程為
的方程為![]() ,即
,即![]() .因為拋物線的準線與
.因為拋物線的準線與![]() 軸的交點
軸的交點![]() 的坐標為
的坐標為![]() ,所以直線
,所以直線![]() 的平行線
的平行線![]() 的方程為
的方程為![]() ,由
,由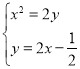 消去
消去![]() 得
得![]() .設
.設![]() 的橫坐標分別為
的橫坐標分別為![]() ,則
,則![]() ,所以
,所以![]() .點
.點![]() 到直線
到直線![]() 的距離為
的距離為 ,所以
,所以![]() .
.


 金牌課堂練系列答案
金牌課堂練系列答案 三新快車金牌周周練系列答案
三新快車金牌周周練系列答案科目:高中數(shù)學 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,短軸長為2;
,短軸長為2;
(1)求橢圓的標準方程;
(2)設橢圓上頂點![]() ,左、右頂點分別為
,左、右頂點分別為![]() 、
、![]() .直線
.直線![]() 且交橢圓于
且交橢圓于![]() 、
、![]() 兩點,點E 關于
兩點,點E 關于![]() 軸的對稱點為點
軸的對稱點為點![]() ,求證:
,求證:![]() .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,在五棱錐P-ABCDE中,△ABE是等邊三角形,四邊形BCDE是直角梯形且∠DEB=∠CBE=90°,G是CD的中點,點P在底面的射影落在線段AG上.
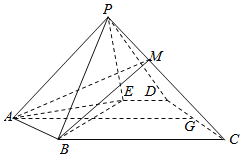
(Ⅰ)求證:平面PBE⊥平面APG;
(Ⅱ)已知AB=2,BC=![]() ,側棱PA與底面ABCDE所成角為45°,S△PBE=
,側棱PA與底面ABCDE所成角為45°,S△PBE=![]() ,點M在側棱PC上,CM=2MP,求二面角M-AB-D的余弦值.
,點M在側棱PC上,CM=2MP,求二面角M-AB-D的余弦值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
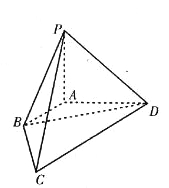
【題目】如圖,在四棱錐![]() 中,已知棱
中,已知棱![]() ,
,![]() ,
,![]() 兩兩垂直,長度分別為1,2,2.若
兩兩垂直,長度分別為1,2,2.若![]() (
(![]() ),且向量
),且向量![]() 與
與![]() 夾角的余弦值為
夾角的余弦值為![]() .
.
(1)求![]() 的值;
的值;
(2)求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知橢圓![]() 經過點
經過點 .離心率
.離心率![]() .
.
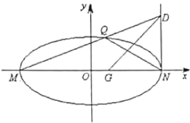
(1)求橢圓C的標準方程;
(2)若M,N分別是橢圓長軸的左、右端點,動點D滿足![]() ,連接MD交橢圓于點Q.問:x軸上是否存在異于點M的定點G,使得以QD為直徑的圓恒過直線QN,GD的交點?若存在,求出點G的坐標;若不存在,說明理由.
,連接MD交橢圓于點Q.問:x軸上是否存在異于點M的定點G,使得以QD為直徑的圓恒過直線QN,GD的交點?若存在,求出點G的坐標;若不存在,說明理由.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在①離心率![]() ,②橢圓
,②橢圓![]() 過點
過點![]() ,③
,③![]() 面積的最大值為
面積的最大值為![]() ,這三個條件中任選一個,補充在下面(橫線處)問題中,解決下面兩個問題.
,這三個條件中任選一個,補充在下面(橫線處)問題中,解決下面兩個問題.
設橢圓![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,過
,過![]() 且斜率為
且斜率為![]() 的直線
的直線![]() 交橢圓于
交橢圓于![]() 兩點,已知橢圓
兩點,已知橢圓![]() 的短軸長為
的短軸長為![]() ,________.
,________.
(1)求橢圓![]() 的方程;
的方程;
(2)若線段![]() 的中垂線與
的中垂線與![]() 軸交于點
軸交于點![]() ,求證:
,求證:![]() 為定值.
為定值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
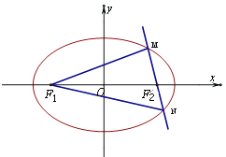
【題目】已知橢圓的焦點坐標為![]() ,
,![]() ,過
,過![]() 垂直于長軸的直線交橢圓于
垂直于長軸的直線交橢圓于![]() 、
、![]() 兩點,且
兩點,且![]() .
.
(Ⅰ)求橢圓的方程;
(Ⅱ)過![]() 的直線
的直線![]() 與橢圓交于不同的兩點
與橢圓交于不同的兩點![]() 、
、![]() ,則
,則![]() 的內切圓的面積是否存在最大值?若存在求出這個最大值及此時的直線方程;若不存在,請說明理由.
的內切圓的面積是否存在最大值?若存在求出這個最大值及此時的直線方程;若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某不透明紙箱中共有4個小球,其中1個白球,3個紅球,它們除顏色外均相同.
(Ⅰ)一次從紙箱中摸出兩個小球,求恰好摸出2個紅球的概率;
(Ⅱ)每次從紙箱中摸出一個小球,記錄顏色后放回紙箱,這樣摸取4次,記得到紅球的次數(shù)為![]() ,求
,求![]() 的分布列;
的分布列;
(Ⅲ)每次從紙箱中摸出一個小球,記錄顏色后放回紙箱,這樣摸取100次,得到幾次紅球的概率最大?只需寫出結論.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com